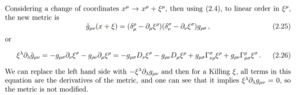Understanding killing vectors and transformations of metric

[dwd40physics]

TL;DR Summary

understanding coordinate transformations of metric and killing vectors

Hi, I am reading through my lecture notes - I haven't formally covered killing vectors but it was introduced briefly in lectures.

Reading through the notes has highlighted something I am not sure about when it comes to co-ordinate transformations.

Q1.Can someone explain how to go from $\tilde{g}_{uv}$ to $g_{uv}$

The bit where it says: we can replace the left hand side with $-\xi^{\lambda}\partial_{\lambda} g_{uv}$

Q2. more basic question how does $\tilde{g}_{uv}$ differ to $g_{uv}$ ? how does a prime function differ from un-primed functions ?

Q3. what does $\xi^{\lambda}\partial_{\lambda} g_{uv} = 0$ tell us ?

thanks :-)

 

[PeterDonis]

Reading through the notes

What notes? Please give a reference.

 

[PeterDonis]

@dwd40physics I have fixed a number of issues with the LaTeX in your OP. Please consult the LaTeX Guide (there is a link at the bottom left of each post window) to help with LaTeX formatting.

 

[dwd40physics]

What notes? Please give a reference.

the image I attached

 

[dwd40physics]

In the notes it says it is a killing vector satisfying the killing equation.

 

[PeterDonis]

the image I attached

That's not a reference. We have no idea where that image came from. A reference means a title/chapter/section of a book or a published paper, or something similar, or a link to an online version of one of those.

 

[dwd40physics]

It's from my university lecture notes... I don't see how a reference resolves this issue. But I can provide a screen shot of whole page if that helps.

 

[PeterDonis]

It's from my university lecture notes

Ok, what university, what course? Are the notes published online?

I don't see how a reference resolves this issue.

First, that's irrelevant; when you are asked for a reference here, you provide it.

Second, whether you see its relevance is immaterial; others might even if you don't, and you can't judge that. For example, if we could read the entire notes instead of just the snippet you posted, we could get useful context about the general treatment of the subject in these notes.

 

[dwd40physics]

Ok, what university, what course? Are the notes published online?First, that's irrelevant; when you are asked for a reference here, you provide it.

Second, whether you see its relevance is immaterial; others might even if you don't, and you can't judge that. For example, if we could read the entire notes instead of just the snippet you posted, we could get useful context about the general treatment of the subject in these notes.

That's a fair challenge, regarding point 2. You're reply did appear to be pedantic rather than try to help with the information I provided. Point 1 comes across rude and unnecessary - people can't always provide a reference they should still be able to helped. The reason I didn't provide a reference is I doubt you would be able to get the lecture notes. To clarify the "reference" it is a course from King's College London 7CCMMS38 - Space-time Structure of Black Holes and the Universe.

 

[dwd40physics]

Here are the relevant pages attached from the lecture notes, thanks.

 

[PeterDonis]

You're reply did appear to be pedantic rather than try to help with the information I provided.

I can't provide any useful response to your actual question unless and until I have the information I have asked for. That's why I asked for it.

Point 1 comes across rude and unnecessary

No, it's a routine request in these forums. You are new here and might not realize that, which is why I am going to the trouble to point it out explicitly. Informing new members of the rules and norms of the forums is one of my jobs as a moderator.

people can't always provide a reference

Sure they can. You could simply answer the questions I have asked.

The reason I didn't provide a reference is I doubt you would be able to get the lecture notes.

Many universities provide copies of lecture notes online, so it's not at all an unreasonable expectation.

To clarify the "reference" it is a course from King's College London 7CCMMS38 - Space-time Structure of Black Holes and the Universe.

That would be this, I take it:

https://www.kcl.ac.uk/abroad/module-options/module?id=79c2e2bd-f9d7-4a26-a4c9-ca16e53360ea

 

[dwd40physics]

ok thanks for your response and clarification of the rules of the forumn. If you are happy with my reference being what course it is from that's fine by me - it isn't a textbook although we have been given wald et al. and Caroll as reco,mmended books but not sure if they will help in this specific example.

 

[dwd40physics]

yes you've found correct course - lecture notes have been produced this year.

 

[PeterDonis]

Here are the relevant pages attached from the lecture notes

Ok, so seeing equation 2.4 it looks like you could invert the transformation $x^\mu \to y^\mu = x^\mu + \xi^\mu$ to obtain $y^\mu \to x^\mu = y^\mu - \xi^\mu$, and then the inverted version of equation 2.4 should give you (to linear order in $\xi^\mu$, the same way equation 2.25 was obtained for the forward transformation) the relation $\xi^\lambda \partial_\lambda \tilde{g}_{\mu \nu} = - \xi^\lambda \partial_\lambda g_{\mu \nu}$ (because of the sign change in the $\xi$ term in the inverse transformation). At least, that seems to me to be what the notes are doing.

As for how $\tilde{g}_{\mu \nu}$ differs from $g_{\mu \nu}$, that's defined by the coordinate transformation; the general form of the relationship is equation 2.4, and equation 2.25 is just equation 2.4 to linear order in $\xi^\mu$ for the particular transformation $y^\mu = x^\mu + \xi^\mu$.

 

[PeterDonis]

If you are happy with my reference being what course it is from that's fine by me

Yes, that's ok since it appears from the course website that the notes are not available online (which is disappointing given how common that is now, but it is what it is). Posting the additional screenshots giving more context was helpful.

ok thanks for your response and clarification of the rules of the forumn. If you are happy with my reference being what course it is from that's fine by me - it isn't a textbook although we have been given wald et al. and Caroll as reco,mmended books but not sure if they will help in this specific example.

Wald's discussion of Killing vector fields is more abstract, and I think his proof that the metric does not change along integral curves of a KVF is different. I don't remember how Carroll treats the subject.

 

[dwd40physics]

yeah I think lots of Uk universities are more tight with uploading accessible content, yeah I wasn't sure if I could have help on the screenshots - I know other books go more abstract as you've said. how does $$\tilde{g}_{uv}$$ differ from $${g}_{\rho\sigma}$$

 

[PeterDonis]

how does $$\tilde{g}_{uv}$$ differ from $${g}_{\rho\sigma}$$

I already answered that in post #14.

 

[dwd40physics]

Ok, so seeing equation 2.4 it looks like you could invert the transformation $x^\mu \to y^\mu = x^\mu + \xi^\mu$ to obtain $y^\mu \to x^\mu = y^\mu - \xi^\mu$, and then the inverted version of equation 2.4 should give you (to linear order in $\xi^\mu$, the same way equation 2.25 was obtained for the forward transformation) the relation $\xi^\lambda \partial_\lambda \tilde{g}_{\mu \nu} = - \xi^\lambda \partial_\lambda g_{\mu \nu}$ (because of the sign change in the $\xi$ term in the inverse transformation). At least, that seems to me to be what the notes are doing.

As for how $\tilde{g}_{\mu \nu}$ differs from $g_{\mu \nu}$, that's defined by the coordinate transformation; the general form of the relationship is equation 2.4, and equation 2.25 is just equation 2.4 to linear order in $\xi^\mu$ for the particular transformation $y^\mu = x^\mu + \xi^\mu$.

is $\tilde{g}_{\mu \nu}$ different from $g_{\mu \nu}$ in terms of it is the same function but expressed in different co-ordinates or are they completely different functions ?

 

[dwd40physics]

Ok, so seeing equation 2.4 it looks like you could invert the transformation $x^\mu \to y^\mu = x^\mu + \xi^\mu$ to obtain $y^\mu \to x^\mu = y^\mu - \xi^\mu$, and then the inverted version of equation 2.4 should give you (to linear order in $\xi^\mu$, the same way equation 2.25 was obtained for the forward transformation) the relation $\xi^\lambda \partial_\lambda \tilde{g}_{\mu \nu} = - \xi^\lambda \partial_\lambda g_{\mu \nu}$ (because of the sign change in the $\xi$ term in the inverse transformation). At least, that seems to me to be what the notes are doing.

As for how $\tilde{g}_{\mu \nu}$ differs from $g_{\mu \nu}$, that's defined by the coordinate transformation; the general form of the relationship is equation 2.4, and equation 2.25 is just equation 2.4 to linear order in $\xi^\mu$ for the particular transformation $y^\mu = x^\mu + \xi^\mu$.

 

[dwd40physics]

i don't get this part:

the relation $\xi^\lambda \partial_\lambda \tilde{g}_{\mu \nu} = - \xi^\lambda \partial_\lambda g_{\mu \nu}$ (because of the sign change in the $\xi$ term in the inverse transformation).

 

[PeterDonis]

is $\tilde{g}_{\mu \nu}$ different from $g_{\mu \nu}$ in terms of it is the same function but expressed in different co-ordinates or are they completely different functions ?

For a general coordinate transformation they would be different functions. For this particular case, where $\xi^\mu$ is a Killing vector field and the transformation is as given, it turns out that $\tilde{g}$ is the same function of the new coordinates as $g$ is of the old coordinates; that is what it means to say that the coordinate transformation does not change the metric.

i don't get this part:

Start with the inverse transformation; apply equation 2.4 to it; then apply the same process that is used to go from equation 2.4 to equation 2.25 for the forward transformation, to come up with the version of equation 2.25 that applies to the inverse transformation. You should find that the signs of the $\xi$ terms are reversed.

Now think about how the LHS of equation 2.26 was obtained from equation 2.25, and how you would obtain a corresponding LHS for the inverse version of 2.26, and what the corresponding LHS looks like.

 

[dwd40physics]

How do I apply inverse to 2.4, I tried but couldn't do it

 

[PeterDonis]

How do I apply inverse to 2.4

Just interchange $x$ and $y$, since the inverse transformation gives $x$ in terms of $y$ instead of $y$ in terms of $x$.

 

[dwd40physics]

Still not sure would this be $g_{\mu\nu}(x) = \frac{\partial{y_\rho}}{\partial{x_\mu}}\frac{\partial{y_\sigma}}{\partial{x_\nu}}\tilde{g}_{\rho\sigma} (y)$ ?

 

[PeterDonis]

@dwd40physics you really need to double check your LaTeX when posting. There is a time window in which you can edit a post once you've made it; please check to see that the LaTeX renders correctly and fix it if it doesn't. I've fixed post #24.

 

[dwd40physics]

sorry i think my computer is bugging apologies

 

[PeterDonis]

Still not sure

Work it out in detail. To start with, you need to understand how they got from equation 2.4 to equation 2.25 for the forward transformation. Do you understand how they did that?

 

[dwd40physics]

Work it out in detail. To start with, you need to understand how they got from equation 2.4 to equation 2.25 for the forward transformation. Do you understand how they did that?

yes I see how you get the forward one, I did the forward one already and you get the kronecka deltas and minus partial derivatives, still not sure how to do LHS

 

[PeterDonis]

I see how you get the forward one

Ok, then do you see how to get from equation 2.25 to equation 2.26 for the forward transformation?

 

[dwd40physics]

do you mean the RHS ?if so yes

 

[PeterDonis]

still not sure how to do LHS

Meaning the LHS of 2.25 for the forward transformation? In equation 2.4, what is $\tilde{g}$ a function of?

 

[dwd40physics]

Meaning the LHS of 2.25 for the forward transformation? In equation 2.4, what is $\tilde{g}$ a function of?

it is a function of y

 

[dwd40physics]

I don't get how to do an inverse transform for this - could you show me some steps.

 

[PeterDonis]

it is a function of y

And what is $y$ for the forward transform? Whatever $y$ is, that is what the argument of $\tilde{g}$ will be on the LHS of equation 2.25.

 

[PeterDonis]

I don't get how to do an inverse transform for this - could you show me some steps.

I already wrote down the inverse transform for you in post #14. Basically you're just exchanging $x$ and $y$; you have the transform for $x$ as a function of $y$ (I gave that in post #14), and you just switch $x$ and $y$ in equation 2.4, and go through the same process you went through for the forward transform.