Nezva
- 46
- 0
Calculate [Lz,L+]
By defintion ladder operators are:
L+=Lx+iLy
L-=Lx-iLy
Important Relations:
LxLy = i\hbarLz, LyLz = i\hbarLx, LzLx = i\hbarLy
Lx = ypz - zpy, Ly = xpz - zpx, Lz = xpy - ypx
To start solving;
[Lz,L+]
Lz - (Lx + iLy) = 0
Multiply through by \hbar:
\hbarLz - \hbarLx + i\hbarLy
The i\hbarLy is equal to LzLx. From this point
I've tried varying approaches in attempt to cancel variable out, but have failed. I have a feeling this problem can be solved easier. Should I try to use spherical coordinates instead of Cartesian? From trying to figure this out I have stumbled upon the answer but I would like to know how to produce the answer.
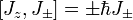
By defintion ladder operators are:
L+=Lx+iLy
L-=Lx-iLy
Important Relations:
LxLy = i\hbarLz, LyLz = i\hbarLx, LzLx = i\hbarLy
Lx = ypz - zpy, Ly = xpz - zpx, Lz = xpy - ypx
To start solving;
[Lz,L+]
Lz - (Lx + iLy) = 0
Multiply through by \hbar:
\hbarLz - \hbarLx + i\hbarLy
The i\hbarLy is equal to LzLx. From this point
I've tried varying approaches in attempt to cancel variable out, but have failed. I have a feeling this problem can be solved easier. Should I try to use spherical coordinates instead of Cartesian? From trying to figure this out I have stumbled upon the answer but I would like to know how to produce the answer.
Last edited by a moderator: