Understanding Shear Force: Uniformly Varying Load in Region EF

[chetzread]

Homework Statement

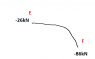
I'm having problem of the shear force at the uniformly varying load at region EF...
Why the shear force isn't -26 +(-30*4/2) at E? but -26 +(-30*4/2) at F?

Homework Equations

The Attempt at a Solution

as we can see the force at region F is 0. the force due to uniformly varying load is (30*4/2) at E...

 

[PhanthomJay]

No. The negative of the area under the load diagram between 2 points is equal to the change in shear between those points. As a check, try drawing a free body diagram of the right section of the beam between a cut just to the left of F and the right end of the beam. What do you get for the shear at that cut section just to the left of F?

 

[chetzread]

No. The negative of the area under the load diagram between 2 points is equal to the change in shear between those points. As a check, try drawing a free body diagram of the right section of the beam between a cut just to the left of F and the right end of the beam. What do you get for the shear at that cut section just to the left of F?

at E, it should be -26 + (-30*4/2) = -86kN, am i right?
As we can see, the weight per unit length start from 0 from right, then to 30kN to the left...So, force above E due to uniformly varying load is (-30*4/2) am I right?

 

[PhanthomJay]

at E, it should be -26 + (-30*4/2) = -86kN, am i right?
As we can see, the weight per unit length start from 0 from right, then to 30kN to the left...So, force above E due to uniformly varying load is (-30*4/2) am I right?

No, please draw free body diagrams. At a section of the right part of the beam cut from E to the right end, look at all the forces acting. The unknown shear V at E, the distributed load down of 30(4)/2 , the reaction load up at F of 136, and the concentrated load of 50 down at G. They must all sum to 0, so V = ??

Or maybe you can look at the left section of the beam from left end to cut at E: unknown V at E, 20(4) down from distributed load, 75 down from load at D, 129 up from reaction at B, so V at E = ??

 

[chetzread]

No, please draw free body diagrams. At a section of the right part of the beam cut from E to the right end, look at all the forces acting. The unknown shear V at E, the distributed load down of 30(4)/2 , the reaction load up at F of 136, and the concentrated load of 50 down at G. They must all sum to 0, so V = ??

Or maybe you can look at the left section of the beam from left end to cut at E: unknown V at E, 20(4) down from distributed load, 75 down from load at D, 129 up from reaction at B, so V at E = ??

the force 30(4/2) is located at E,right? why did the author add it at F ?
So, IMO, it should be -26-(30x4/2) at E, rather than at F...

 

[PhanthomJay]

No you must study up on free body diagrams. I gave you 2 ways to solve for the shear at E using free body diagrams without getting buried by the shear force diagram, but you did not respond with an attempt.

 

[chetzread]

No you must study up on free body diagrams. I gave you 2 ways to solve for the shear at E using free body diagrams without getting buried by the shear force diagram, but you did not respond with an attempt.

well, here's the free body diagram to the left of section E,ya, i get -26kN
but, why the -30(4/2) act at F? Shouldnt it act at the right of region E?

 

[PhanthomJay]

The triangularly distributed load acts between e and f, but the only way to solve for the shear force in the beam at a point along the beam or multiple points is to draw shear force diagrams and free body diagrams or use some calculus tips maybe, but otherwise you can't say what the shear is without using one of the above approaches. I suggest starting with a simple supported beam with a load at the center, or a uniform distributed load, or a cantilver with a load at the end, and determine shears ( and ultimate moments) for those basic cases instead of looking At more advanced stuff like deflections and mohrs circle and indeterminate trusses and such. Get the basics first or else you will be lost in a black hole with no way out. Are you trying to self study? Not easy.

 

[chetzread]

The triangularly distributed load acts between e and f, but the only way to solve for the shear force in the beam at a point along the beam or multiple points is to draw shear force diagrams and free body diagrams or use some calculus tips maybe, but otherwise you can't say what the shear is without using one of the above approaches. I suggest starting with a simple supported beam with a load at the center, or a uniform distributed load, or a cantilver with a load at the end, and determine shears ( and ultimate moments) for those basic cases instead of looking At more advanced stuff like deflections and mohrs circle and indeterminate trusses and such. Get the basics first or else you will be lost in a black hole with no way out. Are you trying to self study? Not easy.

yes, i am doing some self-study now...
I think I can understand the Mohr's circle quite welll.
Now, I am having problem with the distributed load...For the shear force diagram to look like this, the uniformly changing load should start from 0 on the left, and slowly become 30kN/m on the right of EF, am i right? (refer to the diagram )

 

[PhanthomJay]

yes, i am doing some self-study now...
I think I can understand the Mohr's circle quite welll.
Now, I am having problem with the distributed load...For the shear force diagram to look like this, the uniformly changing load should start from 0 on the left, and slowly become 30kN/m on the right of EF, am i right? (refer to the diagram )

No, you are not right. Firstly, if the uniformly changing load were as you show, the support reactions would change and you would have different values in the shear force diagram and the shear curve between E and F would be convex shape facing downward instead of concave shape facing upward. You seem to be assuming that distributed loads can be treated as concentrated point loads, which is incorrect when determining shear forces along the beam. You must instead follow proper procedures when determining shears, as discussed earlier.

 

[chetzread]

No, you are not right. Firstly, if the uniformly changing load were as you show, the support reactions would change and you would have different values in the shear force diagram and the shear curve between E and F would be convex shape facing downward instead of concave shape facing upward. You seem to be assuming that distributed loads can be treated as concentrated point loads, which is incorrect when determining shear forces along the beam. You must instead follow proper procedures when determining shears, as discussed earlier.

the uniformly varying load 'decreases towards the right' , so , the shear force should be -26 - (30*4/2) at E =-86kN and slowly increases to -26kN , where the force due to uniformly varying load is 0 at F...
Why is this wrong?

 

[PhanthomJay]

the uniformly varying load 'decreases towards the right' , so , the shear force should be -26 - (30*4/2) at E =-86kN and slowly increases to -26kN , where the force due to uniformly varying load is 0 at F...
Why is this wrong?

It is wrong because you are not understanding shear force concepts. I think you agreed from looking at a free body diagram of sorts in post 7 that the shear force at E was negative 26. If you look at a free body diagram of the right part of the beam between a section cut just a hair to the left of F to the right end, you should note you have 50 down at G and 136 up at F, implying that the shear force at a hair left of F must be negative 86. Free Body Diagrams are the key to this business.

 

[chetzread]

It is wrong because you are not understanding shear force concepts. I think you agreed from looking at a free body diagram of sorts in post 7 that the shear force at E was negative 26. If you look at a free body diagram of the right part of the beam between a section cut just a hair to the left of F to the right end, you should note you have 50 down at G and 136 up at F, implying that the shear force at a hair left of F must be negative 86. Free Body Diagrams are the key to this business.

yes, i agreed with that.But, I am still not convinced that the graph at region EF look as in the notes...
How if the uniformly varying load is in opposite direction ( i have redrawn it in another direction), is the shear force graph at region EF still the same)?

P/s : I asked this to verify my concept

 

[PhanthomJay]

yes, i agreed with that.But, I am still not convinced that the graph at region EF look as in the notes...
How if the uniformly varying load is in opposite direction ( i have redrawn it in another direction), is the shear force graph at region EF still the same)?

P/s : I asked this to verify my concept

Not the same, see post 10.

 

[chetzread]

E and F would be convex shape facing downward instead of concave shape facing upward.

i am not sure convex downwrads, does it mean this?

 

[PhanthomJay]

yes, the curve shape is correct, but the values won't be the same because you have changed the load diagram and thus support reactions will change so all numerical values change. It will still be true that the shear at F will be the shear at E (whatever it works out to be) minus 60, because as you may recall, he change in shear between E and F is the negative of the area of the triangular distributed loading (- 30 times 4 divided by 2 or neg 60 change).

 

[chetzread]

what do you mean?do you mena the shear force at E will become shear force at F?

 

[PhanthomJay]

no. I'm just saying that if you change the triangular distributed load from 0 increasing to 30 kN/m instead of the given example 30 kN/m decreasing to 0, then you change the cg of that load (1/3 of the way from the fat end of the triangle) and thus support reactions change and thus shear forces change. You do know how to calculate the force reactions, right?

 

[chetzread]

no. I'm just saying that if you change the triangular distributed load from 0 increasing to 30 kN/m instead of the given example 30 kN/m decreasing to 0, then you change the cg of that load (1/3 of the way from the fat end of the triangle) and thus support reactions change and thus shear forces change. You do know how to calculate the force reactions, right?

Ok, I think I can understand, but, why I can't consider it as point load, which at different point along region EF, different downward force act on that particular point?
For example, -60kN downward force act on E , 0kN act on F?

 

[PhanthomJay]

For the purposes of determining reactions at supports, you can consider the triangularly distributed load as a 60 kN downward force acting not at E or F, but at the 1/3 point of the triangle between E and F, at its centroid.

 

[chetzread]

For the purposes of determining reactions at supports, you can consider the triangularly distributed load as a 60 kN downward force acting not at E or F, but at the 1/3 point of the triangle between E and F, at its centroid.

what you said is consider the force at a point only , this is point load , right ?

 

[PhanthomJay]

The resultant of the triangular distributed load is 60 kN acting at the centroid of the triangle. So you can replace that distributed load with a point load acting at the centroid when summing forces and moments to determine reactions. You cannot however replace it with a point load when determining shears and moments between E and F.

 

[chetzread]

You cannot however replace it with a point load when determining shears and moments between E and F.

why?

 

[PhanthomJay]

why?

The shear changes sharply (jumps) at the singularity of the point load P, and gradually and continuously at the distributed load (dV = -w dx). But it is time to accept the solution as correct, and study why, by looking at simpler examples first.