Understanding the Maxwell Stress Tensor

[JD_PM]

Homework Statement

Maxwell Stress Tensor

Relevant Equations

$\vec F = \oint_{s} \vec T \cdot d \vec a - \epsilon \mu \frac{\partial }{\partial t} \oint_{V} \vec S d\tau$

The elecromagnetic force can be expressed using the Maxwell Stress Tensor as:

$$\vec F = \oint_{s} \vec T \cdot d \vec a - \epsilon \mu \frac{\partial }{\partial t} \oint_{V} \vec S d\tau $$

(How can I make the double arrow for the stress tensor $T$?)

In the static case, the second term drops out because the magnetic field is zero.

I have read (from Griffiths) that $T$ represents the force per unit area acting on the surface. But then he states:

Let's see if understand what's going on:

I'd say that the stress tensor on the triangle projected on xy plane would be : $T_{ik}$. Is this correct?

Besides, I am seeking for understanding it. After solving an example exercise

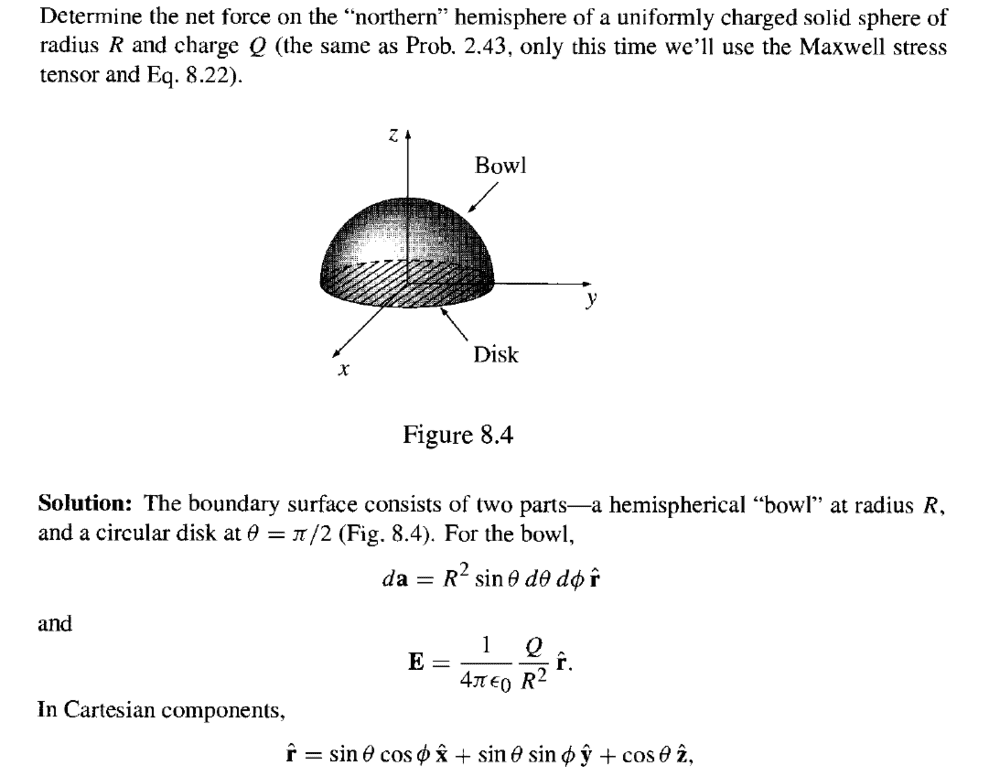
(The exercise is not solved above of course)

But I want to focus on what he states at the end:

How can the tensor 'sniff out what is going inside'?

I don't understand why.

 

[Cryo]

This is the same thing as the
fundamental theorem of calculus $\int^b_a dx\, \frac{df}{dx} = f\left(b\right)-f\left(a\right)$
Stokes theorem: $\int_S d^2 r\, \mathbf{\hat{n}}.\boldsymbol{\nabla}\times\mathbf{F}=\oint_{\partial S} dl \mathbf{\hat{l}}.\mathbf{F}$
Gauss Theorem: $\int_V d^3 r\, \boldsymbol{\nabla}.\mathbf{F}=\oint_{\partial V} d^2 r\, \mathbf{\hat{n}}.\mathbf{F}$

etc. Generally this is known as Generalized Stokes Theorem. The point is that integrating a form ($f$ or $\mathbf{F}$) on the boundary of a manifold ($\partial S$ or $\partial V$) is equal to the integral of the exterior derivative ($\frac{df\left(x\right)}{dx},\, \boldsymbol{\nabla}\times\mathbf{F},\, \boldsymbol{\nabla}.\mathbf{F}$) over that manifold.

In your case $\mathbf{f}=\boldsymbol{\nabla}.\mathbf{T}+\dots$ so

$\mathbf{F}=\int_V d^3 r\, \mathbf{f} = \int_V d^3 r\, \boldsymbol{\nabla}.\mathbf{T}+\dots = \oint_{\partial V} d^2r\, \mathbf{\hat{n}}.\mathbf{T}+\dots$

 

[JD_PM]

Thanks for your reply.

I understand that $\epsilon \mu \oint_{V} \vec S d\tau$ represents the momentum stored in the fields and
$\oint_{s} \vec T \cdot d \vec a$ is the momentum per unit time flowing in through the surface.

 

[Cryo]

I think you are correct, but check your units (just in case)