Understanding the Meaning of "Proper Time"

[Zephaniah]

You can't just talk about one event. You need to talk about the time interval between two events. The actual times on their clocks don't matter. Only the time interval between the events matter. That's what we mean by proper time.

I'm still confused. I'm so sorry. My brain just can't absorb these informations. :(

 

[Zephaniah]

I need to go off-line now. Maybe other members can continue this discussion with you.

Thank you Sir. I hope I can understand all of these later.

 

[robphy]

Given some time like worldline, proper time is the time measured by a clock traveling along that worldline. It is given by $\tau=\int_P \sqrt{1-v^2/c^2}dt$

This might help the OP...
This is an annotated spacetime diagram (a position-vs-time diagram, with time running upwards (by convention)).
Note that we are using the geometry of Minkowski spacetime--not Euclidean geometry (and not the Galilean geometry of the PHY101 position-vs-time graph).

The segment OP is a portion of Alice's worldline (who is at rest in this diagram).
The segment OQ is a portion of Bob's worldline (who is moving with velocity v in this diagram).
According to Alice, events (akin to 'points') P and Q are simultaneous (which is geometrically interpreted by saying that PQ is Minkowski-perpendicular to OP).

It is useful to think in terms of "rapidity" $\theta$ (the Minkowski-angle between two inertial observers).
We have Bob's velocity [according to Alice] as $v=c\tanh\theta$.

For an inertial path OQ through spacetime (the inertial 'worldline' OQ ),
the proper time along that worldline (akin to an arc length along a path) is $\tau_{OQ}$.
Observe that OQ is the hypotenuse of a MInkowski-right triangle.
The adjacent side OP is related by $\tau_{OP}=\left( \cosh\theta\right) \tau_{OQ}$.
So,
$$\begin{eqnarray*}
\tau_{OQ}
&=&\left( \frac{1}{\cosh\theta}\right) \tau_{OP}\\
&=&\left( \sqrt{1-\tanh^2\theta}\right) \tau_{OP}\\
&=&\left( \sqrt{1-(v/c)^2}\right) \tau_{OP}.\\
&=&\left( \sqrt{1-(v/c)^2}\right) t.\\
\end{eqnarray*}$$
The last form is for describing the worldline as a 'function of t'.

If the path of interest is more complicated, the formula is generalized.
For piecewise inertial, add up the separate pieces, $$\tau=\sum_i \sqrt{1-(v_i/c)^2}\Delta t_i.$$
More generally, $$\tau=\int \sqrt{1-(v/c)^2}\ dt.$$
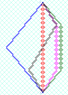
Here's an example of the ClockEffect/TwinParadox.
Suppose that are three worldlines from O to Z,
one inertial,
one with there-and-back speeds of (6/10)c,
and the last has there-and-back speeds of (8/10)c.

The inertial worldline OZ (with velocity 0 in this frame) has proper time 20.
$$\tau_{OPZ}=\sqrt{1-0^2}(20)=20.$$
The piecewise-inertial worldline OQZ has proper time 16.
$$\tau_{OQZ}=\tau_{OQ}+\tau_{QZ}=\sqrt{1-(6/10)^2}(10)+\sqrt{1-(-6/10)^2}(10)=8+8=16.$$
The piecewise-inertial worldline ORZ has proper time 12.
$$\tau_{ORZ}=\tau_{OR}+\tau_{RZ}=\sqrt{1-(8/10)^2}(10)+\sqrt{1-(-8/10)^2}(10)=6+6=12.$$

To visualize this, it is useful to draw a spacetime diagram on rotated graph paper (so that ticks are easier to draw).

Here's a more elaborate example.
I'll leave it to you to work out the numbers.

(See my insights for more information:
https://www.physicsforums.com/insights/spacetime-diagrams-light-clocks/
https://www.physicsforums.com/insights/relativity-rotated-graph-paper/ )

 

[Pencilvester]

You can't just talk about one event. You need to talk about the time interval between two events. The actual times on their clocks don't matter. Only the time interval between the events matter. That's what we mean by proper time.

I'm still confused. I'm so sorry. My brain just can't absorb these informations. :(

The time that you happen to set your watch to is not physically significant. If you are looking at a situation in which there are two observers and a single event, in the absence of additional information about the scenario, the only meaningful (although trivial) statement you can make is that both observers agree that the event occurred. Saying what time each observer determines the event to have happened is arbitrary, as you can set your watch to whatever time you like. More interesting situations compare what two different observers determine the elapsed time to be between two distinct events because that does not depend on what time you set your watch to.

If the two observers are in motion relative to one another, then generally the elapsed coordinate time that each observer measures between the events will differ. However, if there is an object that is present at both events (there doesn’t have to be a physical object, but it makes the scenario more concrete), and if each observer works out the elapsed proper time of the object’s path through spacetime (its worldline) between the two events, then they will both get the same result. If the object happens to be a clock, then the elapsed time that that clock measures is the same as the proper time.

 

[Dale]

Yes Sir. That formula is too complicated for me.

I have changed the level of the thread to B to help respondents answer at the appropriate level of complication. To make this feasible to answer at this level, I will consider only inertial coordinates in flat spacetime with a single dimension of space.

Then the proper time between two events is $\Delta \tau = \sqrt{\Delta t^2-\Delta x^2/c^2}$ where $\Delta t$ is the difference in coordinate time and $\Delta x$ is the difference in coordinate position between the two events and $\Delta \tau$ is the proper time, or the time measured by a clock that travels inertially from one event to the other.

 

[Zephaniah]

Can someone explain this sentence to me? "Any differences between Δt and proper time are not caused by differences in transit times from those space time points to an observer at rest in S." From University Physics book.

 

[Ibix]

Can someone explain this sentence to me? "Any differences between Δt and proper time are not caused by differences in transit times from those space time points to an observer at rest in S." From University Physics book.

With so little context and no actual reference (there are a lot of university physics books and they have a lot of pages - which one, which page?) it's impossible to know. My guess - and it is just a guess - is that the author is stating that time dilation is not merely the delay in clock readings from light travel time (if I look at a clock one light second away, it'll read one second slow because I don't see it as it is now, but as it was when the light left it). It's the discrepancy between clock rates once you have corrected for that lag due to the finite speed of light (which is a changing quantity for a clock moving with respect to the observer).