- 19,865
- 10,853
Definition/Summary
A lens is most often used to focus light rays from an object to form an image. It can also be used to collimate light rays from an object, or to bring a collimated beam of light rays to a focus.
Equations
See "Extended explanation" for definitions of terms.
The well-known Gaussian lens formula uses the focal length to relate the object and image distances for a thin lens:
<br /> \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}<br />
Different notation is often used, so that the Gaussian lens formula is sometimes written:
<br /> \frac{1}{s_o} + \frac{1}{s_i} = \frac{1}{f}<br />
or
<br /> \frac{1}{o} + \frac{1}{i} = \frac{1}{f}<br />
Note that while the letter "o" resembles the number "0", it is NOT (in general) zero.
The thin lens equation or lensmaker's formula uses the lens's surface curvatures and refractive index:
<br /> \frac{1}{d_o} + \frac{1}{d_i} = <br /> (n_{lens}-1)(\frac{1}{R_L}-\frac{1}{R_R})<br />
Note that the right-hand-side is equivalent to 1/f.
The image is magnified (with respect to the size of the object) by the factor
<br /> m = - \ \frac{d_i}{d_o}<br />
A curved mirror surface with radius of curvature R obeys the Gaussian lens formula with
<br /> f = R/2<br />
or, equivalently,
<br /> 1/f = 2/R <br />
Extended explanation
Term definitions:
do (or so or o), the object distance, is the distance from the object to the lens
di (or si or i), the image distance, is the distance from the image to the lens
f is the focal length of the lens
nlens is the refractive index of the lens material
RL and RR are the radii of curvature for the left- and right-hand lens surfaces, respectively.Sign conventions:
do is positive for a real object and negative for a virtual object (See images below).
di is positive for a real image and negative for a virtual image (See images below).
do is ∞ if the incident rays are collimated, and di is ∞ if the outgoing rays are collimated.
f is positive for converging (eg. biconvex and plano-convex) lenses, and negative for diverging (eg. biconcave and plano-concave) lenses.
RL and RR are positive if the "bulge" (convex side) is toward the left, and negative when the bulge is toward the right:
R = ∞ (and 1/R = zero) for a flat surface.
R and f are positive for a concave mirror and negative for a convex mirror.
For the common situation where the object and image are real (do and di both positive), the magnification is negative indicating an inverted image with respect to the object.
If the medium surrounding the lens has a refractive index other than 1, then replace the term
These figures illustrate the three most common situations where the object and image are real or virtual.
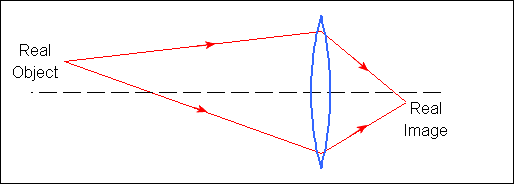
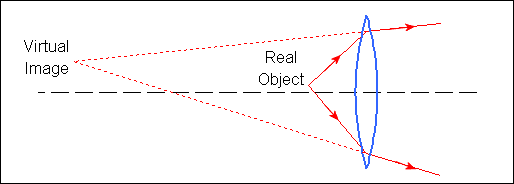
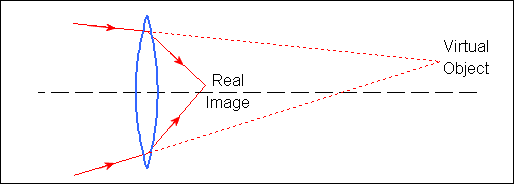
Note: a physical object is always real. Virtual objects can occur in multi-lens systems, when the object for one lens results from the image of a previous lens.
The situation where both object and image are virtual is rare, at least in physics homework exercises. This is possible only for a negative (i.e. diverging) lens.Refractive index for common materials:
Vacuum: n = 1 exactly
Air: n = 1.0003, typically approximated by 1
Water: n = 1.34, average over visible range
Glass: n = 1.5 is typically used in optics homework problems
Fused silica (pure SiO2 glass): 1.46, average over visible range
* This entry is from our old Library feature, and was originally created by Redbelly98.
A lens is most often used to focus light rays from an object to form an image. It can also be used to collimate light rays from an object, or to bring a collimated beam of light rays to a focus.
Equations
See "Extended explanation" for definitions of terms.
The well-known Gaussian lens formula uses the focal length to relate the object and image distances for a thin lens:
<br /> \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}<br />
Different notation is often used, so that the Gaussian lens formula is sometimes written:
<br /> \frac{1}{s_o} + \frac{1}{s_i} = \frac{1}{f}<br />
or
<br /> \frac{1}{o} + \frac{1}{i} = \frac{1}{f}<br />
Note that while the letter "o" resembles the number "0", it is NOT (in general) zero.
The thin lens equation or lensmaker's formula uses the lens's surface curvatures and refractive index:
<br /> \frac{1}{d_o} + \frac{1}{d_i} = <br /> (n_{lens}-1)(\frac{1}{R_L}-\frac{1}{R_R})<br />
Note that the right-hand-side is equivalent to 1/f.
The image is magnified (with respect to the size of the object) by the factor
<br /> m = - \ \frac{d_i}{d_o}<br />
A curved mirror surface with radius of curvature R obeys the Gaussian lens formula with
<br /> f = R/2<br />
or, equivalently,
<br /> 1/f = 2/R <br />
Extended explanation
Term definitions:
do (or so or o), the object distance, is the distance from the object to the lens
di (or si or i), the image distance, is the distance from the image to the lens
f is the focal length of the lens
nlens is the refractive index of the lens material
RL and RR are the radii of curvature for the left- and right-hand lens surfaces, respectively.Sign conventions:
do is positive for a real object and negative for a virtual object (See images below).
di is positive for a real image and negative for a virtual image (See images below).
do is ∞ if the incident rays are collimated, and di is ∞ if the outgoing rays are collimated.
f is positive for converging (eg. biconvex and plano-convex) lenses, and negative for diverging (eg. biconcave and plano-concave) lenses.
RL and RR are positive if the "bulge" (convex side) is toward the left, and negative when the bulge is toward the right:
( R is +
) R is -
) R is -
R = ∞ (and 1/R = zero) for a flat surface.
R and f are positive for a concave mirror and negative for a convex mirror.
For the common situation where the object and image are real (do and di both positive), the magnification is negative indicating an inverted image with respect to the object.
If the medium surrounding the lens has a refractive index other than 1, then replace the term
(nlens - 1)
with(nlens/nmedium - 1)
in the thin lens equation.Real or virtual?These figures illustrate the three most common situations where the object and image are real or virtual.
Note: a physical object is always real. Virtual objects can occur in multi-lens systems, when the object for one lens results from the image of a previous lens.
The situation where both object and image are virtual is rare, at least in physics homework exercises. This is possible only for a negative (i.e. diverging) lens.Refractive index for common materials:
Vacuum: n = 1 exactly
Air: n = 1.0003, typically approximated by 1
Water: n = 1.34, average over visible range
Glass: n = 1.5 is typically used in optics homework problems
Fused silica (pure SiO2 glass): 1.46, average over visible range
* This entry is from our old Library feature, and was originally created by Redbelly98.
Last edited by a moderator: