- #1
JD_PM
- 1,131
- 158
I was reading propulsion chapter 9 of Anderson's Flight book (http://213.230.96.51:8090/files/ebooks/Muhandislik/Anderson J.D. Introduction to flight (8ed., MGH, 2016)(ISBN 9780078027673)(O)(929s) EAs .pdf) and came to Figure 9.18 b) & c), Figure 9.19 (I cannot post the image here due to copyright reasons), which shows the thrust associated to each part of the jet engine.
I want to understand how to physically justify the thrust linked to each part of the jet engine, as shown in Figure 9.19.
It should be justified once the pressure distribution along the engine is understood. Assuming an isentropic, ideal gas, I based my reasoning in Newton's third law.
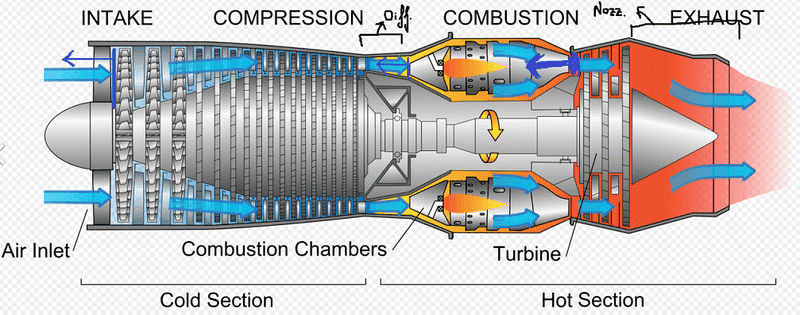
Compressor. The flow exerts pressure (over certain area) on the compressor blades and these exert the same pressure on the flow in the opposite direction, generating thrust. The pressure increases across the compressor because the cross-sectional area decreases through the compressor (the thrust across the compressor ##T_c## increases but I assumed that the latter does so "slower" than the cross-sectional area).
Diffuser. The flow exerts pressure (over certain area) on the tip of the combustion chamber, which exerts the same pressure on the flow in the opposite direction. Despite being a diffuser, we observe that the pressure increases; that has to do with the increase in temperature (this can be seen via the isentropic relation ##\frac{p}{p_0} = \left( \frac{T}{T_0} \right)^{\gamma/(\gamma-1)}##).
Combustion chamber (CC). Here things become interesting. Despite the huge increase in temperature, the pressure experiences a sudden decrease right at the beginning of the CC and the value remains constant throughout. The cross-sectional area cannot justify this so I am still thinking what argument could do.
How can we justify the CC contribution to the thrust? The flow exerts pressure (over certain area) on the the ending part of the combustion chamber, which exerts the same pressure on the flow in the opposite direction.
I have been trying to use the same argument to justify why the thrust linked to the turbine and the convergent nozzle points in the opposite direction but did not come up with a convincing answer yet.
What could be done to optimize the net thrust? I thought the key should be on reducing the thrust linked to the turbine and the convergent nozzle given that they are the responsible for generating an opposite thrust. However, these are necessary in order to increase the flow's speed (we know, due to Mach number-pressure relation (Aerodynamics Anderson EQ. 8.42 https://aviationdose.com/wp-content/uploads/2020/01/Fundamentals-of-aerodynamics-6-Edition.pdf), that if the pressure decreases the speed increases), which is essential in order to generate net thrust.
I find propulsion absolutely fascinating so please feel free to discuss beyond!
I want to understand how to physically justify the thrust linked to each part of the jet engine, as shown in Figure 9.19.
It should be justified once the pressure distribution along the engine is understood. Assuming an isentropic, ideal gas, I based my reasoning in Newton's third law.
Compressor. The flow exerts pressure (over certain area) on the compressor blades and these exert the same pressure on the flow in the opposite direction, generating thrust. The pressure increases across the compressor because the cross-sectional area decreases through the compressor (the thrust across the compressor ##T_c## increases but I assumed that the latter does so "slower" than the cross-sectional area).
Diffuser. The flow exerts pressure (over certain area) on the tip of the combustion chamber, which exerts the same pressure on the flow in the opposite direction. Despite being a diffuser, we observe that the pressure increases; that has to do with the increase in temperature (this can be seen via the isentropic relation ##\frac{p}{p_0} = \left( \frac{T}{T_0} \right)^{\gamma/(\gamma-1)}##).
Combustion chamber (CC). Here things become interesting. Despite the huge increase in temperature, the pressure experiences a sudden decrease right at the beginning of the CC and the value remains constant throughout. The cross-sectional area cannot justify this so I am still thinking what argument could do.
How can we justify the CC contribution to the thrust? The flow exerts pressure (over certain area) on the the ending part of the combustion chamber, which exerts the same pressure on the flow in the opposite direction.
I have been trying to use the same argument to justify why the thrust linked to the turbine and the convergent nozzle points in the opposite direction but did not come up with a convincing answer yet.
What could be done to optimize the net thrust? I thought the key should be on reducing the thrust linked to the turbine and the convergent nozzle given that they are the responsible for generating an opposite thrust. However, these are necessary in order to increase the flow's speed (we know, due to Mach number-pressure relation (Aerodynamics Anderson EQ. 8.42 https://aviationdose.com/wp-content/uploads/2020/01/Fundamentals-of-aerodynamics-6-Edition.pdf), that if the pressure decreases the speed increases), which is essential in order to generate net thrust.
I find propulsion absolutely fascinating so please feel free to discuss beyond!