Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...
I am reading Chapter 6: Topology ... ... and am currently focused on Section 6.1 Topological Spaces ...
I need some help in order to fully understand a statement by Browder in Section 6.1 ... ...
The relevant statements by Browder follow Definition 6.10 and read as follows:
View attachment 9156
View attachment 9157In the above text we read the following:
" ... ... The set $$\overline{E}$$ \ $$E^{ \circ }$$ is referred to as the boundary of $$E$$, and is denoted by $$\text{bdry } E$$; it is easy to see that $$\text{bdry } E = \emptyset$$ if and only if $$E$$ is both open and closed ... ... "My question is as follows:
Can someone explain and demonstrate rigorously how/why $$\text{bdry } E = \emptyset$$ if and only if $$E$$ is both open and closed ... ... ?
Note: I was surprised at Browder's remark above because I was always under the impression (delusion?) that an open set had an empty set as its boundary ...
Help will be appreciated ... ...
Peter======================================================================================The closure of a subset of a topological space is an important notion in the above post so I am providing Browder's definition of closure as well as a basic proposition involving closure ... as follows ...
View attachment 9158
It may help readers of the above post to have access to Browder's fundamental topological definitions ... so I am providing the same as follows ... ...
View attachment 9159
View attachment 9160
View attachment 9161Hope that helps ...
Peter
I am reading Chapter 6: Topology ... ... and am currently focused on Section 6.1 Topological Spaces ...
I need some help in order to fully understand a statement by Browder in Section 6.1 ... ...
The relevant statements by Browder follow Definition 6.10 and read as follows:
View attachment 9156
View attachment 9157In the above text we read the following:
" ... ... The set $$\overline{E}$$ \ $$E^{ \circ }$$ is referred to as the boundary of $$E$$, and is denoted by $$\text{bdry } E$$; it is easy to see that $$\text{bdry } E = \emptyset$$ if and only if $$E$$ is both open and closed ... ... "My question is as follows:
Can someone explain and demonstrate rigorously how/why $$\text{bdry } E = \emptyset$$ if and only if $$E$$ is both open and closed ... ... ?
Note: I was surprised at Browder's remark above because I was always under the impression (delusion?) that an open set had an empty set as its boundary ...
Help will be appreciated ... ...
Peter======================================================================================The closure of a subset of a topological space is an important notion in the above post so I am providing Browder's definition of closure as well as a basic proposition involving closure ... as follows ...
View attachment 9158
It may help readers of the above post to have access to Browder's fundamental topological definitions ... so I am providing the same as follows ... ...
View attachment 9159
View attachment 9160
View attachment 9161Hope that helps ...
Peter
Attachments
-
 Browder - 1 - Defn of Interior 6.10 and Relevant Remarks ... PART 1 ... ....png11.2 KB · Views: 154
Browder - 1 - Defn of Interior 6.10 and Relevant Remarks ... PART 1 ... ....png11.2 KB · Views: 154 -
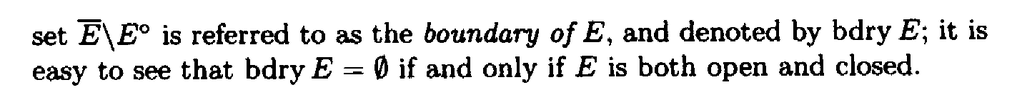 Browder - 2 - Defn of Interior 6.10 and Relevant Remarks ... PART 2 ... .png3.7 KB · Views: 150
Browder - 2 - Defn of Interior 6.10 and Relevant Remarks ... PART 2 ... .png3.7 KB · Views: 150 -
 Browder - Defn of Closure 6.7 and Relevant Propn 6.8 ... .png21 KB · Views: 147
Browder - Defn of Closure 6.7 and Relevant Propn 6.8 ... .png21 KB · Views: 147 -
 Browder - 1 - Start of 6.1 - Relevant Defns & Propns ... PART 1 ... .png15.4 KB · Views: 119
Browder - 1 - Start of 6.1 - Relevant Defns & Propns ... PART 1 ... .png15.4 KB · Views: 119 -
 Browder - 2 - Start of 6.1 - Relevant Defns & Propns ... PART 2 ... .png18.7 KB · Views: 172
Browder - 2 - Start of 6.1 - Relevant Defns & Propns ... PART 2 ... .png18.7 KB · Views: 172 -
 Browder - 3 - Start of 6.1 - Relevant Defns & Propns ... PART 3 ... .png56.3 KB · Views: 155
Browder - 3 - Start of 6.1 - Relevant Defns & Propns ... PART 3 ... .png56.3 KB · Views: 155
Last edited: