Anakratis
- 4
- 0
Hey guys,
So I have a bit of an interesting problem to solve here. I'm trying to calculate the upward repulsion force due to eddy currents created in a conductive surface by a rotating magnetic field. I'm doing this for an undergraduate lab project, and want to be able to provide quantifiable results with equations.
Essentially, I'm placing neodymium bar magnets (in a symmetrical fashion, of course) within an acrylic disc that is attached to a basic servo motor and spins extremely fast above a conductive surface like a copper or aluminum plate. This creates a levitation force due to the eddy currents create at such high angular velocities. I'm trying to find a way to actually calculate this upward force due to these eddy currents created.
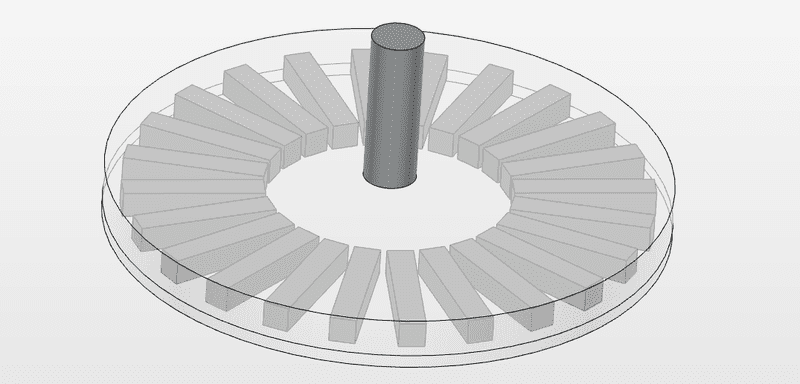
You can look below at the video provided:
I don't even know where to start here, but I do know that we have to somehow use the change in the magnetic field over a conducting surface using a specific linear velocity (which an be converted to RPM). Also using Gauss' law for magnetic field (and the later application of the Lorentz force law):
<br /> \oint\oint{B\cdot dA} = 0<br />
Essentially, I want to be able to input rotations per minute and output the upward force vector, or lift capacity. I realize that this will include many variables, such as the magnetic field strength over the entire surface of the rotor facing the plates. I'm guessing that this is an application of a typical Lorentz force:
F = \frac{d\rho}{dt} = q(E + v \times B)
Where B is the magnetic field strength, and v is the linear velocity of the spinning rotor moving over a surface relative to the surface - however, I'm getting confused over the direction vectors for B, since shouldn't those differ according to the alignment and placement of the magnets themselves (for example, in which direction would B be if I was using something like a Halbach array)? So the direction of F_B seems a little arbitrary to me.
Any thoughts on where to begin?
So I have a bit of an interesting problem to solve here. I'm trying to calculate the upward repulsion force due to eddy currents created in a conductive surface by a rotating magnetic field. I'm doing this for an undergraduate lab project, and want to be able to provide quantifiable results with equations.
Essentially, I'm placing neodymium bar magnets (in a symmetrical fashion, of course) within an acrylic disc that is attached to a basic servo motor and spins extremely fast above a conductive surface like a copper or aluminum plate. This creates a levitation force due to the eddy currents create at such high angular velocities. I'm trying to find a way to actually calculate this upward force due to these eddy currents created.
You can look below at the video provided:
I don't even know where to start here, but I do know that we have to somehow use the change in the magnetic field over a conducting surface using a specific linear velocity (which an be converted to RPM). Also using Gauss' law for magnetic field (and the later application of the Lorentz force law):
<br /> \oint\oint{B\cdot dA} = 0<br />
Essentially, I want to be able to input rotations per minute and output the upward force vector, or lift capacity. I realize that this will include many variables, such as the magnetic field strength over the entire surface of the rotor facing the plates. I'm guessing that this is an application of a typical Lorentz force:
F = \frac{d\rho}{dt} = q(E + v \times B)
Where B is the magnetic field strength, and v is the linear velocity of the spinning rotor moving over a surface relative to the surface - however, I'm getting confused over the direction vectors for B, since shouldn't those differ according to the alignment and placement of the magnets themselves (for example, in which direction would B be if I was using something like a Halbach array)? So the direction of F_B seems a little arbitrary to me.
Any thoughts on where to begin?
Last edited: