member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,
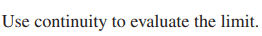
The solution is,

However, I tried to solve this problem using my Graphics Calculator instead of completing the square. I got the zeros of ##x^2 - 2x - 4## to be ##x_1 = 3.236## and ##x_2 = -1.236##
Therefore ##x_1 ≥ 3.236## and ##x_2 ≥ -1.236##
Since ##x_1 > x_2## then,
Therefore ## (x | x ≥ -1.236 ) ## which is ##~(x | x ≥ 1 - \sqrt{5} )~## (sorry curly brackets were not working), however, my domain restriction excludes some other values shown in the solution. Dose anybody please know a way using my method to get those values?
Many thanks!
The solution is,
However, I tried to solve this problem using my Graphics Calculator instead of completing the square. I got the zeros of ##x^2 - 2x - 4## to be ##x_1 = 3.236## and ##x_2 = -1.236##
Therefore ##x_1 ≥ 3.236## and ##x_2 ≥ -1.236##
Since ##x_1 > x_2## then,
Therefore ## (x | x ≥ -1.236 ) ## which is ##~(x | x ≥ 1 - \sqrt{5} )~## (sorry curly brackets were not working), however, my domain restriction excludes some other values shown in the solution. Dose anybody please know a way using my method to get those values?
Many thanks!
Last edited by a moderator: