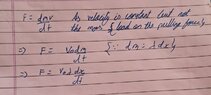Variable mass, uniform body, force -- pulling a massive rope

[Spector989]

Homework Statement

A large rope having linear mass density is being pulled by a horizontal force so that lower portion of rope is at rest and upper portion is moving with constant velocity v as shown in figure. The value of F, is

Relevant Equations

F = dp/dt
F= dmv/dt
dm = lamda dx [ lamda = linear mass density ]
dx/dt = velocity
[ p = momentum] p = mv

So i got some equations but i think i am missing something, my main doubt is what is the relation between dx / dt and v(o) [ here] . Workings in attachment

 

[haruspex]

as shown in figure.

That would help.

 

[Spector989]

That would help.

Oh my bad i forgot to upload the figure

 

[Spector989]

That would help.

Done

 

[haruspex]

This belongs to a class of problems that creates much disagreement. Applying conservation of work and conservation of momentum can seem to lead to different answers.
I would recommend using conservation of work, but bearing in mind that in reality there are subtle reasons why it cannot be fully conserved: losses in bending and straightening the rope, and in work that goes into rotational KE that cannot be fully recovered as linear horizontal KE no matter how elastic the rope.

 

[Spector989]

This belongs to a class of problems that creates much disagreement. Applying conservation of work and conservation of momentum can seem to lead to different answers.
I would recommend using conservation of work, but bearing in mind that in reality there are subtle reasons why it cannot be fully conserved: losses in bending and straightening the rope, and in work that goes into rotational KE that cannot be fully recovered as linear horizontal KE no matter how elastic the rope.

Well i know the reasoning is bad but i guess we can ignore rotational mechanics here as this question is before that was even taught .
And i checked the solution and they wrote v as equal to vo/2 [dx/dt = v , this v ]
As for the conservation of work i will try solving through it , i got a test so will reply later on thanks for the help :)

 

[haruspex]

they took v as vo/2

At a guess, they took the average speed of an element being accelerated from rest to speed v₀ as v₀/2. I believe that will lead to the same answer as given by work conservation.

 

[Spector989]

At a guess, they took the average speed of an element being accelerated from rest to speed v₀ as v₀/2. I believe that will lead to the same answer as given by work conservation.

Why average though

 

[Spector989]

At a guess, they took the average speed of an element being accelerated from rest to speed v₀ as v₀/2. I believe that will lead to the same answer as given by work conservation.

I read the same solution somewhere else but couldn't understand why we took average

 

[haruspex]

I read the same solution somewhere else but couldn't understand why we took average

If you post that whole solution I can check my guess and try to explain why average.

 

[Spector989]

If you post that whole solution I can check my guess and try to explain why average.

 

[haruspex]

Ok, my guess was wrong, but that solution does use the momentum argument.
The author considers an element mass dm going from stationary to moving at speed v₀ in time dt.
Since the upper rope is moving at speed v₀, in time dt it moves to the right v₀dt. But that only advances its left hand end by v₀dt/2, so dm= λv₀dt/2. That's where the v₀/2 comes from.
Since that dm went from 0 to v₀, its momentum increase was λv₀²/2 dt. Hence Fdt=λv₀²/2 dt, so F=λv₀²/2.

However, if we assume work is conserved we get F=λv₀²/4. I'll leave it to you to see how.

So which is right?

It's always risky assuming work is conserved, and one can see ways in which losses occur in this set-up. But to lose half the work?
It turns out the momentum argument is flawed. It assumes the length of rope on the table exerts no force on the rising element; but that is surely false. The rising segment has to rotate about its lower end.
If you push one end of a stick lying on a smooth surface at right angles to the stick its centre of rotation is not the other end of the stick, but a point somewhere between there and the middle of the stick. For it to rotate about the end, you need a bit of a push on that end too.
We can deduce that the resting section of rope must exert some tension on the rising element, thereby assisting F.

On balance, I would say option (4) is closer to the truth than option (3).

 

[Spector989]

Ok, my guess was wrong, but that solution does use the momentum argument.
The author considers an element mass dm going from stationary to moving at speed v₀ in time dt.
Since the upper rope is moving at speed v₀, in time dt it moves to the right v₀dt. But that only advances its left hand end by v₀dt/2, so dm= λv₀dt/2. That's where the v₀/2 comes from.
Since that dm went from 0 to v₀, its momentum increase was λv₀²/2 dt. Hence Fdt=λv₀²/2 dt, so F=λv₀²/2.

However, if we assume work is conserved we get F=λv₀²/4. I'll leave it to you to see how.

So which is right?

It's always risky assuming work is conserved, and one can see ways in which losses occur in this set-up. But to lose half the work?
It turns out the momentum argument is flawed. It assumes the length of rope on the table exerts no force on the rising element; but that is surely false. The rising segment has to rotate about its lower end.
If you push one end of a stick lying on a smooth surface at right angles to the stick its centre of rotation is not the other end of the stick, but a point somewhere between there and the middle of the stick. For it to rotate about the end, you need a bit of a push on that end too.
We can deduce that the resting section of rope must exert some tension on the rising element, thereby assisting F.

On balance, I would say option (4) is closer to the truth than option (3).

Damn , i thought something similar to your first explanation but never about this in such depth . Thanks for the detailed explain:) . I will dicuss option 4 with my sir and get back to you tomorrow thanks a lot .

 

[Spector989]

Ok, my guess was wrong, but that solution does use the momentum argument.
The author considers an element mass dm going from stationary to moving at speed v₀ in time dt.
Since the upper rope is moving at speed v₀, in time dt it moves to the right v₀dt. But that only advances its left hand end by v₀dt/2, so dm= λv₀dt/2.

Could you explain this part i more detail i can't understand it

 

[erobz]

Here is how I came to terms with it after much discussion (very recently here).

The horizontal segment of rope shown above is not accelerating.

Thus;

$$F = F_{dm}$$

To find $F_{dm}$ is the result of accelerating mass $dm = \lambda ~dx$ to velocity $v$ from rest:

$$d F_{dm} = dm~a = dm \frac{dv}{dx} v = \lambda~dx \frac{dv}{dx} v = \lambda v ~ dv $$

We see that implies:

$$ F_{dm} = \lambda \int_{0}^{v} v~dv = \frac{\lambda}{2}v^2 = F $$

This seems to yield the desired outcome.

 

[erobz]

However, if we assume work is conserved we get F=λv₀²/4. I'll leave it to you to see how.

For some reason, I'm not getting that.

The differential work $dW$ done by the force as it moves a distance $dx$ should be the change in kinetic energy of the pulled rope:

$$ dW = F~dx = \frac{1}{2} \lambda ( x + dx) v^2 - \frac{1}{2} \lambda x v^2 = \frac{1}{2}\lambda v^2 dx $$

$$ \implies F = \frac{1}{2}\lambda v^2$$

?

 

[Spector989]

Honestly i am having trouble keeping up with this stuff , i am not used to this level but this is the second question in this section ( we have sections based on difficulty) so sorry if it comes off like i have no clue

 

[erobz]

Honestly i am having trouble keeping up with this stuff , i am not used to this level but this is the second question in this section ( we have sections based on difficulty) so sorry if it comes off like i have no clue

No worries. These problems are responsible for much strife. Take for instance the "chain fountain" debate that occurred on the internet. I don't think its inaccurate to say that these types of problems are still being sorted out.

 

[haruspex]

For some reason, I'm not getting that.

The differential work $dW$ done by the force as it moves a distance $dx$ should be the change in kinetic energy of the pulled rope:

$$ dW = F~dx = \frac{1}{2} \lambda ( x + dx) v^2 - \frac{1}{2} \lambda x v^2 = \frac{1}{2}\lambda v^2 dx $$

$$ \implies F = \frac{1}{2}\lambda v^2$$

?

No, you have overlooked something. Read what I wrote in post #12 regarding dx. I still want @Spector989 to figure it out, so I won't post the details yet.

 

[Spector989]

No, you have overlooked something. Read what I wrote in post #12 regarding dx. I still want @Spector989 to figure it out, so I won't post the details yet.

Alright i will work on it , it might take me some time but i will reply when i am done

 

[Spector989]

To find $F_{dm}$ is the result of accelerating mass $dm = \lambda ~dx$ to velocity $v$ from rest:

How is Fdm result of accelerating mass ? Isn't it a internal force which bounds the wire ?

 

[erobz]

How is Fdm result of accelerating mass ? Isn't it a internal force which bounds the wire ?

It’s is an internal force. But by the third law it is the force that is accelerating the incoming mass(not the mass shown in the diagram) laying in the table.

 

[Spector989]

It’s is an internal force. But by the third law it is the force that is accelerating the incoming mass.

Ooh like tension ?

 

[erobz]

Ooh like tension ?

Yeah

 

[haruspex]

I finally figured out how to analyse the forces.
Assume the rope flexes freely down to some minimum radius of curvature, r. So the rising portion will form a semicircle of that radius.
Each part of it is accelerating towards the centre of curvature, and that acceleration must be the result of tension in the rope. Since all parts have the same magnitude acceleration and same curvature, the tension is constant around the semicircle, namely, F.
Hence the portion of rope still on the ground exerts the same force F, and in the same direction, as is applied to the top part of the rope. That's why the F needed is only half that computed by the official answer.

 

[erobz]

I finally figured out how to analyse the forces.
Assume the rope flexes freely down to some minimum radius of curvature, r. So the rising portion will form a semicircle of that radius.
Each part of it is accelerating towards the centre of curvature, and that acceleration must be the result of tension in the rope. Since all parts have the same magnitude acceleration and same curvature, the tension is constant around the semicircle, namely, F.
Hence the portion of rope still on the ground exerts the same force F, and in the same direction, as is applied to the top part of the rope. That's why the F needed is only half that computed by the official answer.

This kind of makes me think of the scenario:

Where the pulley is advancing at half the velocity at which the free end of the rope is pulled. Is that basically what is going on?

 

[haruspex]

This kind of makes me think of the scenario:

View attachment 317992
Where the pulley is advancing at half the velocity at which the free end of the rope is pulled. Is that basically what is going on?

Yes.

 

[Spector989]

This kind of makes me think of the scenario:

View attachment 317992
Where the pulley is advancing at half the velocity at which the free end of the rope is pulled. Is that basically what is going on?

This example makes stuff pretty clear

 

[Spector989]

I finally figured out how to analyse the forces.
Assume the rope flexes freely down to some minimum radius of curvature, r. So the rising portion will form a semicircle of that radius.
Each part of it is accelerating towards the centre of curvature, and that acceleration must be the result of tension in the rope. Since all parts have the same magnitude acceleration and same curvature, the tension is constant around the semicircle, namely, F.
Hence the portion of rope still on the ground exerts the same force F, and in the same direction, as is applied to the top part of the rope. That's why the F needed is only half that computed by the official answer.

But won't dm = lambda dx / 2 , so if we use the former argument, we will get the official answer , and how is internal force assisting F which appeared due to F , it's kind of hard to wrap my head around it

 

[haruspex]

how is internal force assisting F

It is not an internal force. The portion lying on the ground is presumed not to slide, so something external is retaining it, like friction.