Velocity of an Electron between Two Plate

[doggydan42]

Homework Statement

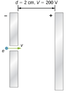
An electron enters a region between two large parallel plates made of aluminum separated by a distance of 2.0 cm and kept at a potential difference of 200 V. The electron enters through a small hole in the negative plate and moves toward the positive plate. At the time the electron is near the negative plate, its speed is Assume the electric field between the plates to be uniform, and find the speed of electron at (a) 0.10 cm, (b) 0.50 cm, (c) 1.0 cm, and (d) 1.5 cm from the negative plate, and (e) immediately before it hits the positive plate

2. Homework Equations
If V is the potential difference and K is the kinetic energy, then
$$-q\Delta V = \Delta K = \frac{1}{2} m(v^2-v_0^2)
\\\Delta V = \int_{a}^b \vec E \bullet d{\vec l}$$

The Attempt at a Solution

To solve, I used the first formula. q is the charge of an electron, $\Delta V$ is given, and m would be the mass of an electron. Though my problem is that this means that the velocity does not depend on the distance from the plate.

Thank you in advance

 

[phyzguy]

You are given the potential difference between the plates and told that the electric field is uniform between the plates. Your formula for ΔV is correct, but the integration limits a and b will change depending on where you are evaluating the velocity.

 

[doggydan42]

You are given the potential difference between the plates and told that the electric field is uniform between the plates. Your formula for ΔV is correct, but the integration limits a and b will change depending on where you are evaluating the velocity.

If the integration limits change, then what would be the potential difference the problem gave?

Would the potential difference be used to find the electric field across d, where d is the distance between the plates? Then, the potential difference becomes $\Delta V = Er$ for distance r from the negative plate.

Thank you in advance.

 

[phyzguy]

If the integration limits change, then what would be the potential difference the problem gave?

The potential difference given in the problem is across the whole d=2cm distance between the plates, as shown by the arrows.

Would the potential difference be used to find the electric field across d, where d is the distance between the plates? Then, the potential difference becomes $\Delta V = Er$ for distance r from the negative plate.

Correct. In this case, what is E, given the potential difference V and the plate separation d?