Venusian Angular Units (vau): Describe & Calculate Sun's Parallax

[RingNebula57]

Homework Statement

Like humans, astronomers of Venus use the same method for definitions of parallaxes and of
parsec but measure them in different (their own) units. For example, the distance to Sirius equals to 19.6
vpc (19.6 venusial parsec).
- Describe the most evident system of angular units used by astronomers of Venus.
- Calculate the venusial diurnal parallax of the Sun and write the answer in “vau” (venusial angular units –
the common angular units for astronomers of Venus).
Note: citizens of Venus have two hands (as humans), and 7 fingers at each hand.

2. Homework Equations

The Attempt at a Solution

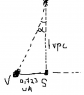
The distance between Sirius and Sun is equal to 2,6 pc. If we take the definition of the parsec and aply it to Venus, we find out that 1 vpc=0,723 pc.

[/B]So distance from Sun to Sirius is d=2,6 pc = 3,596 vpc

Ok ,so now I have to relate 19,6 vpc with 3,596vpc , but how?( I might think about the ideea of numerical base conversion, because of the fingers, but it still doesn't work for me). In the picture below alpha=1".

 

[jbriggs444]

You have the raw data that you need already figured out.

It is 19.6 vpc's to Sirius using the Venusian units of arc. It would 3.596 vpc's using the Earth units of arc. That's a ratio of about 5.4 to one (5.45 if we allowed three sig figs).

One whole circle is 1296000 arc seconds using the Earth standard for arc seconds. It would be 7063200 arc seconds using the Venusian measure. The first task is to figure out the Venusian unit of arc. That's basically a numbers game -- coming up with a set of "base 14" numbers whose product is roughly 7063200

My first try was 14² * 14² * 14². That comes out close -- 7.5 million rather than 7.1 million. But that's only a one sig fig match. The source data in the problem is good to at least two sig figs.

My next try played around with the idea that 6*14 = 84 and that's a pretty nice choice for the number of minutes in a degree or the number of seconds in a minute if you have 7 fingers on each hand. Can we make that fit? How many Venusian degrees would there then be in a circle? 7063200/84/84 = 1001.

Assume that the number of degrees in a circle is a multiple of 14. Divide 1001 by 14 and you get 71.5.

72 is a nice even multiple of a lot of numbers. Make that guess. Then the number of Venusian arc seconds in a circle is 72*14 * 84 * 84 = 7112448. That's a two sig fig match. It's all guesswork and a two sig fig match is all one can trust from two sig fig input data anyway. May as well assume that it's correct.

 

[RingNebula57]

Thank you, I got it