Vibrations of a rod and vertical spring with 60 degree angle offset

[garethLovell]

Homework Statement

University 3rd year mechanics problem

Relevant Equations

equations of motion (Sum of Moments = Inertia x angular acceleration)
ma + kx = 0 (a = x (double dot))
m * (theta double dot) + k * (theta) = 0

This is the problem I am working on at the moment. The question states that the bar is at rest in this state. At a 60 degree angle to the horizontal and supported by the vertical spring at B.

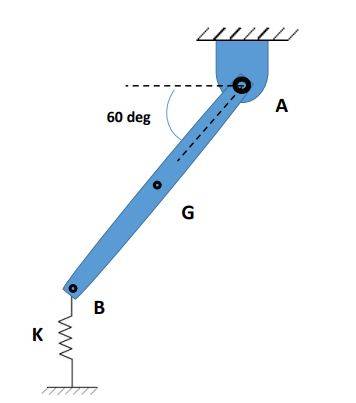
Small oscillations are introduced and I am required to find the equation of motion and the natural frequency.

omega(n) = squareroot(k/m)

I have a image of the progress I have made so far. I am a little muddled because I am not sure if, that by the bar being at rest at this angle, if the deflected angle (theta) is added to the 60 or if theta is treated as the whole angle.

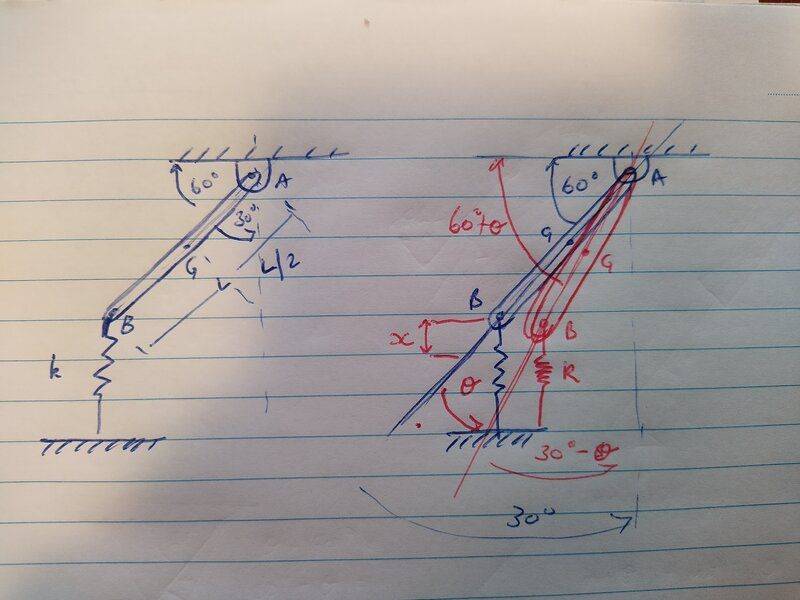
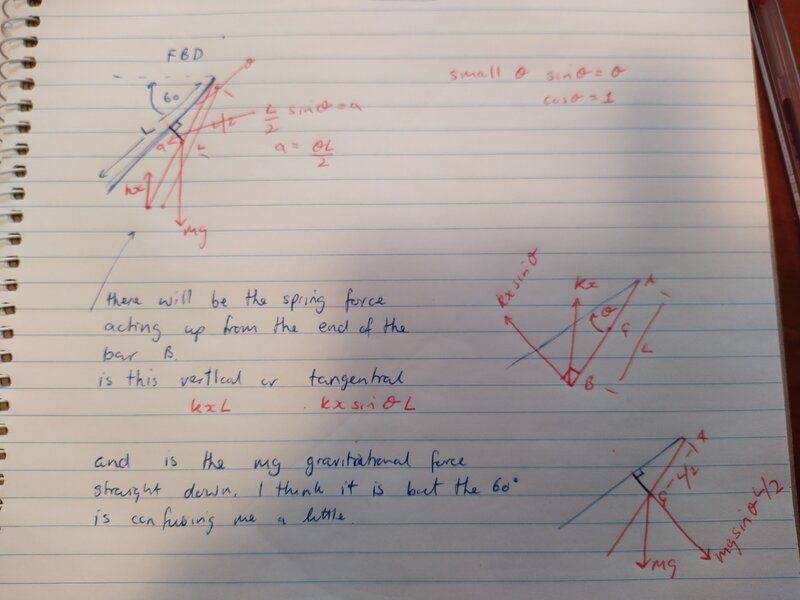
am I close to the right track or way off?

regards,
gareth

 

[Lnewqban]

Welcome!
I can see some problems in your work and with the used equations.

Look for "The Physical Pendulum" at this link:
https://courses.lumenlearning.com/boundless-physics/chapter/periodic-motion/

Please, also see:
http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html#rlin

http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html#c1

Could you generate a free body diagram of the oscillating bar?
Let's forget about the movement and focus on the static forces acting on that bar in the initial position.

 

[garethLovell]

Welcome!
I can see some problems in your work and with the used equations.

Could you generate a free body diagram of the oscillating bar?
Let's forget about the movement and focus on the static forces acting on that bar in the initial position.

Thank you so much for your reply. I've had a look at the content you suggested.
Should I be focusing on the rotational inertia of the rod? Also I drew the fbd. I think the only forces working on the rod at rest are the force of gravity and the spring opposite to the gravitational force to keep it in equilibrium. It is suspended at 60 degrees so the spring force is kxcos60? I've drawn the kx vertical by mistake.

Does mg=-kxcos60?

Again thankyou so much.

Regards Gareth

 

[Lnewqban]

We don't know the value of either k or x at priori.
We know that the center of mass of the bar is located halfway, regardless its positioning angle.
We also know that the bar is supported at its ends by a spring and a pivot.
The spring can only handle vertical loads (compression and tension, we can safely assume).
The pivot can handle both, vertical and horizontal loads, but no moment or torque about itself.

Based on that, we have the spring and the pivot equally sharing the load of the weight of the bar (purely vertical reactive forces) and no horizontal forces, to be represented in our free body diagram (FBD).
You can then have directions and magnitudes of three forces in the FBD representing the initial position of our bar.

In order to simplify the problem and the solution, I would assume that the spring is sufficiently long respect to the dimensions of the rod, in such a way that oscillations of small amplitude do not deform it sideways and its reactive force (which increases linearly as the rod deviates from this original balanced, non-oscillating condition) remains more or less vertical.

Correct, we have to consider the angular inertia of the oscillating system.
You are very welcome :)

 

[garethLovell]

We don't know the value of either k or x at priori.
We know that the center of mass of the bar is located halfway, regardless its positioning angle.
We also know that the bar is supported at its ends by a spring and a pivot.
The spring can only handle vertical loads (compression and tension, we can safely assume).
The pivot can handle both, vertical and horizontal loads, but no moment or torque about itself.

Based on that, we have the spring and the pivot equally sharing the load of the weight of the bar (purely vertical reactive forces) and no horizontal forces, to be represented in our free body diagram (FBD).
You can then have directions and magnitudes of three forces in the FBD representing the initial position of our bar.

In order to simplify the problem and the solution, I would assume that the spring is sufficiently long respect to the dimensions of the rod, in such a way that oscillations of small amplitude do not deform it sideways and its reactive force (which increases linearly as the rod deviates from this original balanced, non-oscillating condition) remains more or less vertical.

Correct, we have to consider the angular inertia of the oscillating system.
You are very welcome :)

thanks Lnewqban. I think I have it sorted now, that lumenlearning content was fantastic. I have revised my answers and I believe I understand what you have said here.

my FBD has Mg straight down from the CoM (point G) and the spring restoring force (-k * theta) vertically up from point B. The third force you've stated, is that the normal force on the pivot, straight up or am I correct with the k*theta*cos60?

this is what I have right now.

i didn't draw in the third force, i don't know where that is acting on the system.

regards,
gareth

 

[Lnewqban]

That third force is acting directly on the pivot, but because it has no distance or lever respect to that pivot, it creates no torque and may be disregarded in this problem.
The components of the bar's weigh and spring forces that are perpendicular to the bar (mg cos 60 and 0.5mg cos 60) are the ones that we should multiply by the distance's L/2 and L.

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/torq2.html

https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/10-6-torque/