Voltage of residential Air-Conditioner thermostats

[fourthindiana]

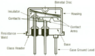
I am reading a book titled Refrigeration and Air-Conditioning Technology, and I am now at a chapter in Refrigeration and Air-Conditioning Technology about Automatic Control Components and Applications. I am confused about a sentence in a section of this chapter regarding thermostats. The thermostat section of the book compares and contrasts motor winding thermostats and space temperature thermostats. Motor winding thermostats are thermostats on the compressors of air-conditioners.

Space temperature thermostats are thermostats for residential/commercial air-conditioning. The purpose of this thread is to ask about one sentence in this paragraph that I don't understand. I believe that the entire paragraph that contains this confusing sentence and the entire paragraph before the confusing sentence should be included for context.

I will boldface and color the confusing sentence green in the quote. Here is the quote and the confusing sentence I am asking about:

"Another difference between the two thermostats is the medium they sense. The motor-winding thermostat must be in close contact with the motor winding. It is fastened to the winding itself. The space temperature is mounted on a wall and responds to random air currents passing over it. Another important design concept is the current carrying characteristics of the various controls. In the space temperature application, the stopping or starting of a heating system, such as a gas or oil furnace, involves stopping or starting low-voltage (24 volt) components and line-voltage (115-volt or 230-volt) components. The gas or oil furnace normally has a low-voltage gas valve or relay and a line-voltage blower motor.

There is no firm rule for using one voltage or another in any specific application. However, the stopping and starting of a 3-hp compressor requires a larger switching mechanism than the one used to control a simple gas valve. A 3-hp compressor could operate with a running amperage of 18A and a starting amperage of 90 A, whereas a simple gas valve might draw only 0.5 A. If a bimetal were large enough to carry the current for a 3-hp compressor, the control would be so large that it would be slow to respond to temperature changes. This is one reason for using low-voltage controls to stop and start high-voltage components."

It sounds to me like in the sentence I colored green, the authors are talking about an analog thermostat with a bimetal to control the thermostat. Why would a large bimetal in a thermostat be slower to respond to temperature changes than a small bimetal in a thermostat? The bimetal is a piece of brass attached back to back with steel. I am aware of the fact that a longer bimetal will bend further than a shorter bimetal, but the degrees of bending would be the same. Let me make an example. In the example, the stationary part of the bimetal will be the reference line of an angle. I don't see why it would take longer for a, say, 10 inch long bimetal to bend from 180 degrees to 160 degrees than it would take a 5 inch long bimetal to bend from 180 degrees to 160 degrees.

If a bimetal were large enough to carry the current for a 3-hp compressor, how would the large size of the control cause the control to be slow to respond to temperature changes?

 

[.Scott]

The primary problem is with the thermal mass. The same amount of heat transfer will result in a smaller change in temperature for a more thermally massive part. The concern would be that the compressor would be damaged before sufficient heat was transferred to a 90 Amp bimetallic thermal switch to cause it to trip.

BTW: When a bimetallic strip is used for heating a space, a small heating resistor is almost always included to compensate for the sluggish response of the switch. As the room heats up, the resister heats the thermostat - not enough to turn the thermostat off if the room is still very chilly, but enough to prevent the temperature of the room form overshooting the target.

 

[gneill]

Why would a large bimetal in a thermostat be slower to respond to temperature changes than a small bimetal in a thermostat?

Because a larger piece of material will have a larger heat capacity than a smaller one. It takes longer to boil a large pot of water than a small one using the same stove element. Think of it like "thermal inertia".

 

[AZFIREBALL]

It is all related to the mass of the controlling device element. If it is large, it has more mass. It will take longer to change its temperature to match the surrounding environment thus slowing the switching action. A small element switching device will sense the environment temperature change quicker due to its having less mass to heat/cool. The mass between an element that can withstand the inrush of a 3 hp motor would be over 100 times larger than the mass of a small element needed to operate a low current (24 volt) relay used to start the large motor.

 

[fourthindiana]

.Scott and gneill, thank you for your responses, but I still don't fully understand this.

If you have both a regular sized Chevrolet Camaro that is approximately 20 feet long and a toy 2 inch long replica of a Chevrolet Camaro (and the toy replica is composed of the same type of metal as the real Camaro) sitting on the same driveway all day and the temperature has been 90 degrees for several hours, I would expect both the approx. 20 feet real Camaro and the 2 inch toy Camaro to both be around 90 degrees. It might take more heat to heat up the real Camaro than the 2 inch toy Camaro, but the real Camaro has 20 feet more surface area to absorb heat than the toy, so both the real Camaro and the 2 inch long toy are going to be about the same temperature.

Because a larger piece of material will have a larger heat capacity than a smaller one. It takes longer to boil a large pot of water than a small one using the same stove element. Think of it like "thermal inertia".

I understand the concept of thermal inertia for a pot of water on a stove, but I don't understand this in this context. If you have one bimetal strip, composed of brass and steel, that is 1 inch long and 1 cm wide and you have another bimetal strip, composed of brass and steel, that is 2 inches long and 1 cm wide, I understand that it would take twice as many BTU's of heat to heat the 2 inch long bimetal than the 1 inch long bimetal. However, the 2 inch long bimetal will have twice the surface area of the 1 inch long bimetal. Therefore, I would expect the 2 inch long bimetal to absorb twice as many BTUs per second as the 1 inch long bimetal. In a thermostat, the BTUs in the air of a room are large enough that it's not like a stove's heating element where the amount of BTUs produced by the stove is very finite and limiting. In my example, why wouldn't the 2 inch long bimetal in a thermostat not absorb twice as many BTUs per second as the 1 inch long bimetal?

 

[gneill]

You're assuming that the bimetal is the only part of the device. The case and mounting components would also have to grow in size to accommodate the larger sensor. Then the growth is not just surface area of the bimetal. Take a look at the construction of a typical thermostat switch for equipment:

Borrowed from https://forum.digikey.com/t/disc-bimetallic-thermostats/680

The surface area of the housing increases not only for the contact area where the device is in contact with the heat source, but also the rest of the housing which will be immersed in the (presumably) lower temperature surrounding air.

 

[fourthindiana]

gneill, I agree with you that the entire thermostat would have to increase in size, not just the bimetal. However, it still seems to me that in a residential air-condioner, unless the enclosed space of the house is extremely tiny, the enclosed space of the house would usually have enough BTUs to make it so that the thermal inertia of a 230V thermostat and a 24 volt thermostat would be a negligible difference. Am I missing something else?

 

[.Scott]

If you have both a regular sized Chevrolet Camaro that is approximately 20 feet long and a toy 2 inch long replica of a Chevrolet Camaro (and the toy replica is composed of the same type of metal as the real Camaro) sitting on the same driveway all day and the temperature has been 90 degrees for several hours, I would expect both the approx. 20 feet real Camaro and the 2 inch toy Camaro to both be around 90 degrees. It might take more heat to heat up the real Camaro than the 2 inch toy Camaro, but the real Camaro has 20 feet more surface area to absorb heat than the toy, so both the real Camaro and the 2 inch long toy are going to be about the same temperature.

OK. Let's say that on one hand (your larger hand) you have an Earth size planet with an interior temperature of about 6000C and in the other hand you have a small replica of Earth, say 4 inches in diameter - exactly proportional also with an interior temperature of 6000C.
Which one will burn your hand faster?

 

[gneill]

A 230 V thermostat would require more mass due to the larger switch contacts, more insulation for safety, beefier wire connectors, etc.

 

[jrmichler]

I understand the concept of thermal inertia for a pot of water on a stove, but I don't understand this in this context. If you have one bimetal strip, composed of brass and steel, that is 1 inch long and 1 cm wide and you have another bimetal strip, composed of brass and steel, that is 2 inches long and 1 cm wide, I understand that it would take twice as many BTU's of heat to heat the 2 inch long bimetal than the 1 inch long bimetal. However, the 2 inch long bimetal will have twice the surface area of the 1 inch long bimetal. Therefore, I would expect the 2 inch long bimetal to absorb twice as many BTUs per second as the 1 inch long bimetal. In a thermostat, the BTUs in the air of a room are large enough that it's not like a stove's heating element where the amount of BTUs produced by the stove is very finite and limiting. In my example, why wouldn't the 2 inch long bimetal in a thermostat not absorb twice as many BTUs per second as the 1 inch long bimetal?

In your example, you are assuming that the two bimetal strips have the same length and thickness. In that case, the larger strip has twice the surface area and twice the mass. The strip exchanges heat to/from the environment through the surface. Since the ratio of surface area to volume is the same for both strips, they will respond to ambient temperature changes at the same rate.

On the other hand, if you make a bimetal strip larger by scaling it, then all dimensions increase in the same proportion. Make the larger strip twice as long, twice as wide, and twice as thick. In that case, the larger strip has four times the surface area, and eight times the volume. Each square inch of surface area now has to transfer heat to twice as much volume (thermal mass) as the smaller strip. That larger strip will take longer to respond to changes in the ambient temperature. This is an example of the cube-square law.

 

[russ_watters]

If you have both a regular sized Chevrolet Camaro that is approximately 20 feet long and a toy 2 inch long replica of a Chevrolet Camaro (and the toy replica is composed of the same type of metal as the real Camaro) sitting on the same driveway all day and the temperature has been 90 degrees for several hours, I would expect both the approx. 20 feet real Camaro and the 2 inch toy Camaro to both be around 90 degrees. It might take more heat to heat up the real Camaro than the 2 inch toy Camaro, but the real Camaro has 20 feet more surface area to absorb heat than the toy, so both the real Camaro and the 2 inch long toy are going to be about the same temperature.

Surface area and volume are *not* proportional to length. Assuming length, width and height scale the same, surface area is a square function and volume a cube function. So larger objects take longer to change temperature than smaller ones.

 

[AZFIREBALL]

Try this...Place a 1 mm lead ball in a 1500 degree oven at the same time you place a 10 bar of lead in the same oven . Which one will melt first?