SUMMARY
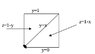
The discussion focuses on calculating the volume and mass of a pyramid-shaped object in the first octant, defined by the planes x + z = 1 and y + z = 1, with a density function of p(x,y,z) = xyz. The correct approach involves using a double integral to account for the varying limits of integration based on the geometry of the pyramid. The final mass was determined to be m = 1/120, after correctly establishing the bounds for x, y, and z during integration.
PREREQUISITES
- Understanding of triple integrals in multivariable calculus
- Familiarity with the concept of density functions
- Knowledge of geometric shapes and volume calculations
- Ability to set up and evaluate integrals with variable limits
NEXT STEPS
- Study the method of setting up triple integrals for varying limits
- Learn about the geometric interpretation of integrals in three dimensions
- Explore the application of density functions in mass calculations
- Practice problems involving integration of piecewise functions
USEFUL FOR
Students in calculus, particularly those studying multivariable calculus, as well as educators looking for examples of integration in three dimensions and applications of density functions in mass calculations.