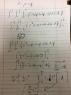- #1
Mohamed Abdul
Homework Statement
Find the z -coordinate of the center of mass of the first octant of a sphere of radius R centered at the origin. Assume that the sphere has a uniform density.
Homework Equations
Mass = Integral of the density function
Center of mass for z = Integral of density * z divided by mass
The Attempt at a Solution
I have two questions with this problem, one being whether I should use a triple or double integral, and what the value inside my integral should be. Since the sphere has uniform density, I assume the integrand should be 1, but I'm not sure.
I at least know that my bounds should be 0<r<R and 0<theta<pi/4 since I'm operating in the first octant.