Volume of a Solid- 3D Calculus

[fridakahlo]

Homework Statement

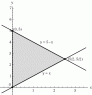
Find the volume of the given solid.
Bounded by the planes
z = x, y = x, x + y = 5 and z = 0

Homework Equations

V = [PLAIN]http://www.webassign.net/wastatic/wacache6cdd60ea0045eb7a6ec44c54d29ed402/watex/img/integral.gif[PLAIN]http://www.webassign.net/wastatic/wacache6cdd60ea0045eb7a6ec44c54d29ed402/watex/img/integral.giff(x,y) dA
For a type I integral: dA=dy*dx
and the domain is: a<x<b, g1(x)<y<g2(x)

For a type II integral: dA=dx*dy
and the domain is: c<y<d, h1(y)<x<h2(y)

3. The Attempt at a Solution
I chose to evaluate this integral by making region D as a type I integral, therefore my domain is as follows:
0<x<5/2 & x<y<5-x
My f(x,y)=x
dA=dy*dx

Is it possible to do this as a type II integral? That way my limits would look a lot nicer, but I don't know what my h1(y) and h2(y) functions would be.

 

[Buzz Bloom]

Hi fridakahlo:

I think that when you calculate a volume by integration you need an integral of the form
V = ∫∫∫ f(x,y,z) dV = = ∫∫∫ f(x,y,z) dx dy dz

Hope this helps.

Regards,
Buzz

 

[haruspex]

Hi fridakahlo:

I think that when you calculate a volume by integration you need an integral of the form
V = ∫∫∫ f(x,y,z) dV = = ∫∫∫ f(x,y,z) dx dy dz

Hope this helps.

Regards,
Buzz

No, a volume integral would just be ∫∫∫dxdydz, no need for a function. But in this case fridakahlo is effectively assuming the z integral has been done, leaving either ∫∫fdxdy or ∫∫dydx.

@fridakahlo , yes you can do the x integral before y, but you would need to split the outermost integral into two ranges, y<2.5 and y>2.5.