Volume-pressure equation for an expanding ideal gas

[MatinSAR]

Homework Statement

How do I find the volume-pressure equation for an expanding ideal gas for the figure below?

Relevant Equations

pV=nRT

There is no atmosphere pressure.

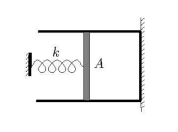
My work :
pA=k(x-x₀) => pA=(k/A)(V-V₀)

But this should be false beccause I want to use W=∫PdV to find work done by the gas but my final anwer is wrong ...
Please guide me where my mistake is if you have enough time. Thanks.

 

[Chestermiller]

Please show more details of what you did. Is this expansion by adding heat at constant temperature? Please provide an exact word-for-word statement of the problem.

 

[MatinSAR]

Is this expansion by adding heat at constant temperature?

It just said that we heat the gas slowly.

Please provide an exact word-for-word statement of the problem.

We heat the gas slowly so that it goes from (P1,V1) to (P2,V2). What is the work done on the gas?
We can use Hook's law for the spring. Piston is light(=forget mass of it).

Please show more details of what you did.

I want to find the equation between pressure and volume.
And I don't know why this is wrong :
pA=k(x-x1) => pA=(k/A)(V-V1)

 

[MatinSAR]

pA=(k/A)(V-V1)

I think I have founded the problem. It should be (p-p₁)A=(k/A)(V-V₁).
Is it true?

 

[Chestermiller]

I think I have founded the problem. It should be (p-p₁)A=(k/A)(V-V₁).
Is it true?

yes

 

[MatinSAR]

yes

Thank you for your help and time.

 

[erobz]

I'm having some doubts on this one?

Ignoring atmospheric pressure on the spring side seems like bit of blunder IMO. The spring would initially have to be compressed at $x_o$.Bypassing that issue, I think it's understood to be in a state of "quasistatic equilibrium" this implies that the forces are balanced across the piston.

$$ - k ( x - x_o ) + F_g = 0 $$

$$ \implies P_x = \frac{k}{A}( x - x_o )$$

you can see that the absolute pressure in the gas must be 0 at $x = x_o$ in the absence of atmospheric pressure...is that really ok? Don't we have to be at absolute zero in temperature initially for this to be possible? can we have a gas at absolute 0 temp? Some of the question I have.

In terms of volume $V\llap{-}$, just multiply through by $A$:

$$ P_x A = \frac{k}{A}( V\llap{-}_x - V\llap{-}_o )$$

$$ \boxed{ P_x = \frac{k}{A^2}( V\llap{-}_x - V\llap{-}_o ) }$$

What am I missing?

 

[Chestermiller]

View attachment 320900

I'm having some doubts on this one?

Ignoring atmospheric pressure on the spring side seems like bit of blunder IMO. The spring would initially have to be compressed at $x_o$.Bypassing that issue, I think it's understood to be in a state of "quasistatic equilibrium" this implies that the forces are balanced across the piston.

$$ - k ( x - x_o ) + F_g = 0 $$

$$ \implies P_x = \frac{k}{A}( x - x_o )$$
In terms of volume $V\llap{-}$, just multiply through by $A$:

$$ P_x A = \frac{k}{A}( V\llap{-}_x - V\llap{-}_o )$$

$$ \boxed{ P_x = \frac{k}{A^2}( V\llap{-}_x - V\llap{-}_o ) }$$

What am I missing?

In my judgment, the confusion with this problem is yours.

The problem statement says that the atmospheric pressure is zero. This is the same as saying that the device is contained within a vacuum chamber. Who says that this is not allowed?

If the atmospheric pressure is zero, this means that the spring is under preload compression so that the forces on both sides of the piston are initially equal. Therefore, $$P_1A=A\frac{nRT_1}{V_1}=\frac{k}{A}(V_1-V_0)$$where $V_0$ would be the volume at which the sprig is unextended. At all other times, the forces on both sides of the piston also match: $$P=\frac{nRT}{V}=\frac{nRT_1}{V_1}+\frac{k}{A^2}(V-V_1)$$

So what's the problem?

 

[erobz]

In my judgment, the confusion with this problem is yours.

Quite likely.

So what's the problem?

One thing, if this is happening in the vacuum of space we have to have a gas at some initial volume $V\llap{-}_o$ ( zero pre-compressed spring state) with absolute zero temperature (with regards to the ideal gas law).

 

[Chestermiller]

Quite likely.

One thing, if this is happening in the vacuum of space we have to have a gas at some initial volume $V\llap{-}_o$ ( zero pre-compressed spring state) with absolute zero temperature (with regards to the ideal gas law).

No. Vo is the chamber volume at which the spring is unextended. This is geometric, and independent of the gas.

 

[erobz]

No. Vo is the chamber volume at which the spring is unextended. This is geometric, and independent of the gas.

Ahh, there is no gas in the chamber when $V\llap{-} = V\llap{-}_o$. I guess that is the plausible alternative I was missing.

Thank You.