What angle to pull the yo-yo under so it doesn't roll?

[Ryker]

Homework Statement

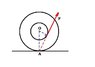
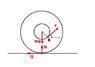
The yo-yo is made of two wheels, connected by a short beam (the cross-section of the beam looks like the letter "H"), around which wire is wrapped up. Let the yo-yo be stationary on a desk. What is the angle ß in relation to the said desk (see picture) that we must gently pull the wire so as not to cause the yo-yo to roll?

The picture is really small, so to give a legend of sorts: "r" is used for the diameter of the inner circle, "R" for the bigger one, "ß" for the angle and "F" for the force with which we pull the wire.

Homework Equations

The Attempt at a Solution

I was really lost on this one, until I looked up the solution and tried to make sense of it. The following is the best I can come up with.

So there's three forces acting on the yo-yo, which is the force with which we're pulling the wire, the yo-yo's weight and the force of the desk (comprised of static friction and a force opposing the weight of the yo-yo). Since the yo-yo is not moving, they, along with the torque they cause, must equal zero.

So we first look at our force "F", which can be seen as a result of two components, one being parallel to the desk and the other perpendicular to it. For that we sketch a triangle or a rectangle. The force parallel to the desk points in the opposite direction to the force of static friction and must therefore cause equal torque. Said torque must be in linear relation to the diameter of the inner circle "r", because that's where the force "F" has its hold. The force "F" itself, too, must be in such a relation to the total force of the desk to cause the same torque. Therefore, as the desk touches the yo-yo at outer rim of a circle with the diameter "R", the force "F" is in linear relation to "R".

Looking again at the triangle (or rectangle) again we find that the solution to the problem is:

$$\cos (\beta) = \frac{r}{R}$$

I don't know, seems a bit shaky to me, so that's why I thought maybe someone can look at the problem and see if I went into the right direction with my thinking.

 

[hikaru1221]

I don't get your explanation, but the result is correct. A simpler way: Consider torque about the point of contact.

 

[Ryker]

Hmm, could you elaborate on that? I was trying to do that, but couldn't figure out my way about it.

 

[hikaru1221]

How will the moments of weight and force by the ground about that point be? In order that the yo-yo doesn't move, how should the moment of the applied force (or tension) about the point of contact be?

 

[Ryker]

I figured the weight wouldn't have any impact since it's right on the axis. But the ground would exert torque with the handle of "R". And "F" should exert the exact opposite torque to that, but with a handle of "r". I still can't get it to that cosine relationship, though.

 

[hikaru1221]

I figured the weight wouldn't have any impact since it's right on the axis. But the ground would exert torque with the handle of "R". And "F" should exert the exact opposite torque to that, but with a handle of "r". I still can't get it to that cosine relationship, though.

That's when you consider the center as the point you calculate torque with respect to. But what if you consider another point - the point of contact, or the lowest point of the yo-yo?

 

[Ryker]

Hmm, well I'm looking at the picture and I've been going over this for hours (pondering that last thing you pointed out, as well), but I still don't see the cosine relationship. I mean, I'm really trying, but I just seem to be stuck. I appreciate that you're trying to give me hints, but I think I'm getting really frustrated with the problem, because I just can't see why cosine and I can't get to that triangle. Could you perhaps just tell me how you got to that answer? This isn't even homework (I'm revising stuff we did in high school 7 years ago as preparation for my second degree in Physics), so it wouldn't be cheating. And, honestly, I can't get my head around this no matter how hard I try.

 

[hikaru1221]

Forget that cosine, forget triangles. Keep in your mind only the rule: If a thing is in equilibrium, the total torque about any point = zero.

The point I referred to is A. The torque by weight about A = 0, the torque by force by the ground about A = 0. So if the yo-yo stays at rest, torque by tension about A = 0 too. That corresponds to the case I drew in the picture.

 

[Ryker]

Hey, thanks a lot, I finally get it now. Though I tried setting up that point of contact as the center now and again couldn't get the answer. I figure I have to balance out the torque from the weight and the torque from the force of the ground, but after sketching out multiple circles I seem to be unable to get it right. Could you please help me with that, as well?

edit: On second thought, what did you mean by point of contact - contact with ground or the point where our pulling force is applied? Since you obviously spelled it out for me for the former, it's the latter which I'm now having trouble with.

 

[hikaru1221]

Sorry for the confusion. The point of contact I mentioned is A - the point of contact with the ground.

I don't quite get it. So you mean, you have understood how to solve the problem using the point A and want to find a solution with another point? If so then what is that another point you want to consider?

Oh, keep in mind one thing: howsoever you solve the problem, the rules never change: If one thing is in equilibrium:
_ Total force on it = 0
_ Total torque on it about any point = 0

 

[Ryker]

I don't quite get it. So you mean, you have understood how to solve the problem using the point A and want to find a solution with another point? If so then what is that another point you want to consider?

Yeah, I thought you meant the problem is easily solvable using *either* the lowest point of the yo-yo or the point where the force with which you pull hits the inner circle (I thought this is what you meant by point of contact). However, when trying the latter version, I'm getting nowhere, since, due to only our force "F" being irrelevant as far as torque is concerned, I would now have to balance out the force and torque of both weight and the ground. Or do you see an "easy" solution at that point, as well? If yes, could you describe how you got it (that diagram was really helpful)?

Oh, keep in mind one thing: howsoever you solve the problem, the rules never change: If one thing is in equilibrium:
_ Total force on it = 0
_ Total torque on it about any point = 0

Thanks, though this is actually something I had in mind from the get-go, I just couldn't apply it. I think what got me was that I kind of forgot that you can proloung the line our force "F" is on to get the handle (which needed to be 0 in our case, as it turned out). Basically, I got really confused by getting those perpendicular components that are needed to calculate torque, but I now see where I went wrong. So, again, thanks for your help!

 

[hikaru1221]

So you understand my solution, right?

Okay, if you want to avoid the point A and consider the other point of contact B (where the wire meets the yo-yo), then it's a bit more complicated. Let Q denote the friction force and N denote the normal force. Because the yo-yo is in equilibrium:
_ The total force on it = 0:

(1) $$Fcos\beta = Q$$

(2) $$Fsin\beta + N = mg$$

_ The total torque about B = 0:

(3) $$mgrsin\beta = Nrsin\beta + Q(R-rcos\beta)$$

From (1) and (2): $$(mg-N)cos\beta = Qsin\beta$$

From (3): $$(mg-N)rsin\beta = Q(R-rcos\beta)$$

From the 2 above equations:

$$r\frac{sin\beta}{cos\beta} = \frac{R-rcos\beta}{sin\beta}$$

$$rsin^2\beta = Rcos\beta - rcos^2\beta$$

$$r(sin^2\beta + cos^2\beta) = Rcos\beta$$

Notice that $$sin^2\beta + cos^2\beta = 1$$, we get: $$cos\beta = r/R$$

 

[Ryker]

So you understand my solution, right?

Heh, I really though I did. I mean, that first solution now really seems so obvious and, like I said, it wasn't not knowing about what the torque and force sum should be, but how to apply it.

Okay, if you want to avoid the point A and consider the other point of contact B (where the wire meets the yo-yo), then it's a bit more complicated. Let Q denote the friction force and N denote the normal force. Because the yo-yo is in equilibrium:
_ The total force on it = 0:

(1) $$Fcos\beta = Q$$

(2) $$Fsin\beta + N = mg$$

_ The total torque about B = 0:

(3) $$mgrsin\beta = Nrsin\beta + Q(R-rcos\beta)$$

From (1) and (2): $$(mg-N)cos\beta = Qsin\beta$$

From (3): $$(mg-N)rsin\beta = Q(R-rcos\beta)$$

From the 2 above equations:

$$r\frac{sin\beta}{cos\beta} = \frac{R-rcos\beta}{sin\beta}$$

$$rsin^2\beta = Rcos\beta - rcos^2\beta$$

$$r(sin^2\beta + cos^2\beta) = Rcos\beta$$

Notice that $$sin^2\beta + cos^2\beta = 1$$, we get: $$cos\beta = r/R$$

Yeah, that does seem a bit more complicated, but after going through it you've done a fine job explaining it. Here again I thought it would be as easy as the first path, so I got frustrated when there was no simple solution like above and just gave up on it, thinking I wouldn't be able to solve it.

Well, thanks again for your kind help, it really is greatly appreciated!