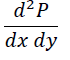What Are the Dimensions for Force and Distance in This Problem?

  • Thread starter Thread starter pyroknife
  • Start date Start date
  • Tags Tags
    Dimensions
AI Thread Summary
The discussion focuses on determining the dimensions for force (P) and distance (x, y, z) in a physics problem. The dimensions for force are established as (ML/T^2), where M represents mass, L is length, and T is time. There is confusion regarding the differentiation of force with respect to distance, specifically whether dP/dx results in dimensions of M/T^2. The user questions if the second derivative would yield the same dimensions and seeks clarification on the dimensional analysis of derivatives and ratios. The conversation highlights the complexities of applying calculus concepts to dimensional analysis in physics problems.
pyroknife
Messages
611
Reaction score
4

Homework Statement


Let P represent a force and x, y, and z represent distances. Determine the dimensions for each of the quantities listed below.

I attached the problem I need help with. (it's a small picture)
So I'm a bit confused since the it involves both dx and dy.

The dimensions for P is (ML/T^2)
Where M=mass
L=length
T=time

Then I have to differentiate it twice but with two different variables. Since x and y refer to distances and the only distance found in that equation is L.

Would that mean the dimensions for dP/dx = M/T^2 ?

If so, would that mean the answer to the 2nd derivative still be the same answer since they're differentiating between different variables? (I'm not sure if I worded this right, but I remember from Calc III something similar)
On a side note. I took calculus quite a while ago so some of this I might have forgotten.
The picture I provided, that is not equivalent to (dP/dx)*(dP/dy) right?
 

Attachments

  • Untitled.png
    Untitled.png
    907 bytes · Views: 406
Last edited:
Physics news on Phys.org
A derivative is the limit of a certain ratio. It has the same dimensions as the ratio. What dimensions does the ratio have?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Direction of a spring's force in more than one dimension
Replies
6
Views
2K
What are the forces on a cell in a tree vs on the surface of a tree
Replies
4
Views
1K
Time it Takes for a Transverse Pulse to Travel a Distance "L" Up a Cable Against Gravity?
Replies
13
Views
1K
Dimensional Analysis of an oscillation
Replies
3
Views
3K
Forces applied to a spring-loaded gas pedal
Replies
7
Views
1K
Time dependant Potential Energy in ion trap
Replies
1
Views
2K
Golf club 🏌️and ball ⛳ impulse problem
Replies
19
Views
2K
Shortest distance along the shore and into the lake
Replies
6
Views
908
Weight of gold chain when dropped on a weighing scale
Replies
12
Views
2K
Hydrostatic pressure in a tilted tube
Replies
6
Views
3K

Hot Threads

Recent Insights

Back
Top