MisterX
- 758
- 71
Background
For which of the invertible transformations (\mathbf{q}, \mathbf{p}) \leftrightarrow(\mathbf{Q}, \mathbf{P})
\mathbf{Q}(\mathbf {q}, \mathbf {p}, t)
\mathbf{P}(\mathbf{q}, \mathbf {p}, t)
is it so that for every Hamiltonian \mathcal{H}(\mathbf {q}, \mathbf {p}, t) there is a \mathcal{K} such that
\dot{Q}_i = \frac{\partial\mathcal{K}}{\partial P_i} \;\;\;\;\;\;\;\; \dot{P}_i = -\frac{\partial\mathcal{K}}{\partial Q_i}\; ?
Stationary action should correspond, and that condition is met if
\sum p_i\dot{q}_i - \mathcal{H} = \sum P_i\dot{Q}_i - \mathcal{K} + \frac{dF}{dt},
since integrating \frac{dF}{dt} results in something only dependent of the endpoints.
Question
Consider this part of Goldstein's Classical Mechanics.
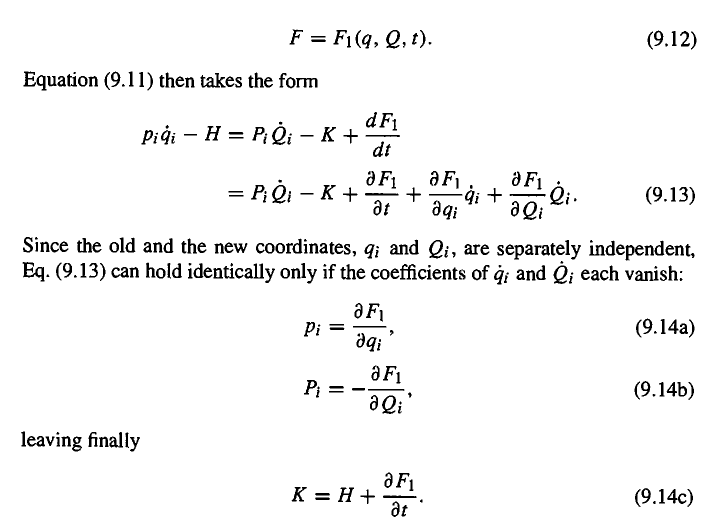
rearranging 9.13 to make this clear:
\mathcal{K} = \mathcal{H} + \frac{\partial F_1}{\partial t} + \sum_i \dot{Q}_i\left(P_i - \frac{\partial F_1}{\partial Q_i} \right) + \sum_i \dot{q}_i\left(\frac{\partial F_1}{\partial q_i} - p_i\right)
I guess I might like this explained a more. Why aren't we able to to have the coefficients of \dot{q}_i or \dot{Q}_i be non-zero, and have the difference absorbed into \mathcal{K} ?
For which of the invertible transformations (\mathbf{q}, \mathbf{p}) \leftrightarrow(\mathbf{Q}, \mathbf{P})
\mathbf{Q}(\mathbf {q}, \mathbf {p}, t)
\mathbf{P}(\mathbf{q}, \mathbf {p}, t)
is it so that for every Hamiltonian \mathcal{H}(\mathbf {q}, \mathbf {p}, t) there is a \mathcal{K} such that
\dot{Q}_i = \frac{\partial\mathcal{K}}{\partial P_i} \;\;\;\;\;\;\;\; \dot{P}_i = -\frac{\partial\mathcal{K}}{\partial Q_i}\; ?
Stationary action should correspond, and that condition is met if
\sum p_i\dot{q}_i - \mathcal{H} = \sum P_i\dot{Q}_i - \mathcal{K} + \frac{dF}{dt},
since integrating \frac{dF}{dt} results in something only dependent of the endpoints.
Question
Consider this part of Goldstein's Classical Mechanics.
rearranging 9.13 to make this clear:
\mathcal{K} = \mathcal{H} + \frac{\partial F_1}{\partial t} + \sum_i \dot{Q}_i\left(P_i - \frac{\partial F_1}{\partial Q_i} \right) + \sum_i \dot{q}_i\left(\frac{\partial F_1}{\partial q_i} - p_i\right)
I guess I might like this explained a more. Why aren't we able to to have the coefficients of \dot{q}_i or \dot{Q}_i be non-zero, and have the difference absorbed into \mathcal{K} ?