What Determines the Order of Rotations for a Gyro?

[Trying2Learn]

TL;DR

This could be another idiotic question (let's hedge our bets and say it is). Still, regardless of Tait or Euler angles, what is the order of applying the rotations?

This could be a whole lot of nothing... however...

Here are two figures used in gyroscopic analyses.

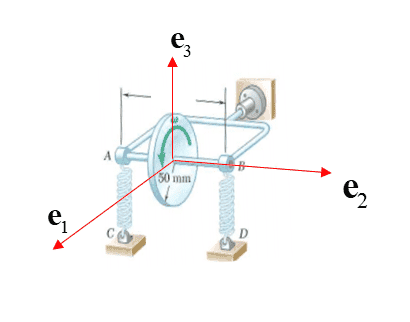
• On the left, is a model for an inertial guidance system on an airplane. As the airplane precesses (about the vertical 3-axis), and as the disk spins about the local 2-axis, there is an induced nuation, restricted by the springs, to measure the direction of the plane.
  • To model the system on the LEFT, I use the Tait angles in order: 3-axis, 1-axis, 2-axis. I can do this, and it all works out.
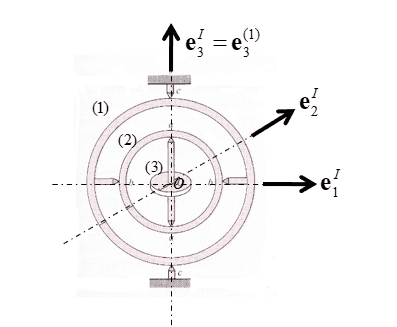
• On the right, is a standard Cardan Gyroscope
  • To model the system on the RIGHT, I use the Euler angles in order: 3-axis, 1-axis, 3-axis. I can do this, and it all works out.

So far, so good, I understand.

Now suppose I remove all the structures/gimbals that "inform" me (or guide me) in the order of rotations? Suppose I delete everythig except the disk mass itself and leave it hanging in space.

What, in these stripped-down problems "informs" me of the order in which I apply the rotations?
Or, is the supporting structure itself, the thing that informs me? (I think this is true)

Thus, for the one on the RIGHT, why could I not model it in THIS order?
(It is still a 3, 1 3 Euler angle family)

1. Spin of disk about 3-axis
2. Nutation of disk about 1-axis
3. Precession of disk about the local 3-axis

If I analyzed this in the order I just wrote, then, after the nutation, there is no remaining vertical axis about which to "precess" (so maybe that is the issue)

If I do it "correctly" and precessed, then nutated, there does remain the body disk axis about which to spin.

What is it about the stripped down disk, that in both figures, the SPIN is to the LAST of the rotations applied?

 

[Lnewqban]

The spinning of a body at high angular velocity is the source of any precession; therefore, it must be first.
That fast spinning of a mass induces an angular momentum vector, which resists any change to its spatial orientation.

If an external moment applied on the spinning body forces a modification of that spatial orientation, a reactive moment appears and an additional rotation in a different direction is induced by that external moment.

The function of the gimbals shown in the second picture Is to isolate the spinning (at high rpm's) disc from any external moment, so it remains rotating in the same exact spatial orientation.

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/rotv2.html#rvec4

 

[vanhees71]

Here's my write-up about some introductory theory of the spinning top. I hope it's of some use!

https://itp.uni-frankfurt.de/~hees/pf-faq/spinning-top.pdf