- #1
- 2,168
- 193
I am trying to understand the meaning of the Likelihood function or the value of the Likelihood itself. Let us suppose we are tossing coins and we have a sample data given as
$$\hat{x} = \{H,H,T,T,T,T\}$$
For instance in this case the Likelihood Function can be given as
$$L(\theta|\hat{x}) = C(6,2)\theta^2(1-\theta)^4 = 15\theta^2(1-\theta)^4$$
The function looks like this
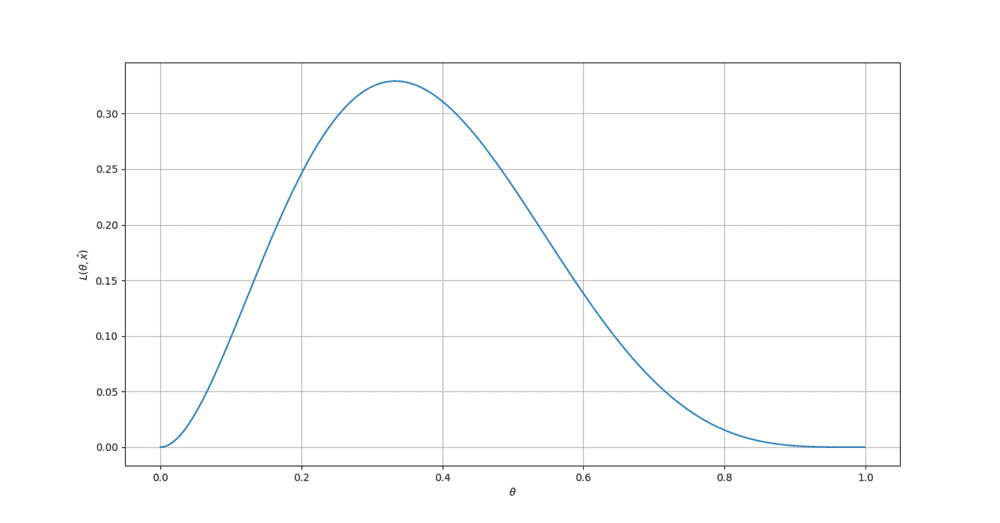
Now, my question is what does this graph tells us ? We can say that for ##\theta = 0.333##, ##L(\theta|\hat{x}) ## is maximum.
In general it seems to me that the Likelihood is way of obtaining the best parameters that describes distribution the given data. If we change the parameters that describe the distribution, we change the Likelihood.
We know that for fair coin ##\theta_{True} = 0.5##. So my question is does the Likelihood means for this data (##\hat{x}##), the best parameter that describes the fairness of the coin is ##0.3333## (i.e when the Likelihood is maximum) ? We know that if the coin is truly fair, for a large sample we will obtain the true ##\theta## parameter (i.e ##N \rightarrow \infty, \theta \rightarrow \theta_{True}##).
In general, I am trying to understand the meaning of the likelihood. Does the Likelihood is a way to obtain the best ##\theta## parameter that describes the distribution for the given data. But, depending on the given data the ##\theta## may not be the true ##\theta## (i.e., ##\theta \neq \theta_{True}## for the given data) .
(For a Gaussian ##θ = {µ,σ}##, for a Poisson distribution, ##θ = λ## and for a binomial distribution, ##θ = p##, the probability of success in one trial.)
$$\hat{x} = \{H,H,T,T,T,T\}$$
For instance in this case the Likelihood Function can be given as
$$L(\theta|\hat{x}) = C(6,2)\theta^2(1-\theta)^4 = 15\theta^2(1-\theta)^4$$
The function looks like this
Now, my question is what does this graph tells us ? We can say that for ##\theta = 0.333##, ##L(\theta|\hat{x}) ## is maximum.
In general it seems to me that the Likelihood is way of obtaining the best parameters that describes distribution the given data. If we change the parameters that describe the distribution, we change the Likelihood.
We know that for fair coin ##\theta_{True} = 0.5##. So my question is does the Likelihood means for this data (##\hat{x}##), the best parameter that describes the fairness of the coin is ##0.3333## (i.e when the Likelihood is maximum) ? We know that if the coin is truly fair, for a large sample we will obtain the true ##\theta## parameter (i.e ##N \rightarrow \infty, \theta \rightarrow \theta_{True}##).
In general, I am trying to understand the meaning of the likelihood. Does the Likelihood is a way to obtain the best ##\theta## parameter that describes the distribution for the given data. But, depending on the given data the ##\theta## may not be the true ##\theta## (i.e., ##\theta \neq \theta_{True}## for the given data) .
(For a Gaussian ##θ = {µ,σ}##, for a Poisson distribution, ##θ = λ## and for a binomial distribution, ##θ = p##, the probability of success in one trial.)