What does this voltmeter measure?

[Granger]

Homework Statement

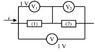
Consider the following circuit where i(t) is sinusoidal and exists across both components. (1) is an inductor and (2) is a capacitor. The ideal voltmeters measure effective value. What is the value measured by V2:

[![enter image description here][1]][1] [1]: https://i.stack.imgur.com/d7OfJ.png

The correct answer should be 2V

Homework Equations

3. The Attempt at a Solution [/B]

My attempt.
I know we can only apply KVL using phasors. The current phasor should be $$Ie^{j\theta}$$

The voltage across the inductor is $$\omega LIe^{j(\theta+\pi/2)}=V_1e^{j(\theta+\pi/2)}$$
The voltage across the capacitor is $$\frac{I}{\omega C}e^{j(\theta+-\pi/2)}=V_2e^{j(\theta-\pi/2)}$$

And the voltage across both components $$(\omega L-\frac{1}{\omega C})Ie^{j(\theta+-\pi/2)}=Ve^{j(\theta+\pi/2)}$$

And so applying KVL we get to

$$Ve^{j(\theta+\pi/2)}=V_1e^{j(\theta+\pi/2)}+V_2e^{j(\theta-\pi/2)}$$
$$Ve^{j\pi/2)}=V_1e^{j(\pi/2)}+V_2e^{j(-\pi/2)}$$

And dividing everything by $$\sqrt{2}$$

$$V_{eff}e^{j\pi/2)}=V_{1eff}e^{j(\pi/2)}+V_{2eff}e^{j(-\pi/2)}$$

Substituting by the known values

$$1e^{j\pi/2)}=1e^{j(\pi/2)}+V_{2eff}e^{j(-\pi/2)}$$
$$0=V_{2eff}e^{j(-\pi/2)}$$

And so $$V_{2eff}=0$$.

However the correct answer should be +2V.

Can someone help me to figure out my mistake? It's probably a conceptual mistake. Thanks!

 

[cnh1995]

Instead of the lengthy mathemtical approach, why not try the phasor approach?
Draw the phasor diagram of the circuit.
What is the phase difference between V_L and V_c in a series circuit?

 

[Granger]

Instead of the lengthy mathemtical approach, why not try the phasor approach?
Draw the phasor diagram of the circuit.
What is the phase difference between V_L and V_c in a series circuit?

Hi!
Oh yes that's the better approach, I didn't thought about it, thanks!
The phase difference between the voltages across the inductor and the capacitor is \pi.
Since the overall effective voltage is 1 that leaves us with two options: the voltage on the capacitor is zero (this is the case when the overall voltage and the inductor voltage are on phase) or the voltage on the capacitor is 2V (and then the overall voltage is on phase with the capacitor voltage). Since the capacitance is not zero we go with the second option.
Is that right?

 

[cnh1995]

Since the capacitance is not zero we go with the second option.
Is that right?

Yes.