- #1
Ulysees
- 516
- 0
Does the theorem still hold true, but triangle sides are curves?
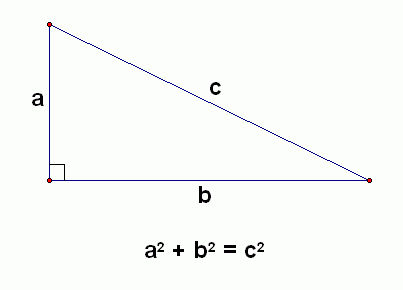
Ulysees said:
Ulysees said:
tiny-tim said:If you put cos ~ 1 + ( ^2)/2, you get … ?
tiny-tim said:ooh … sorry … my ~ meant "is approximately", and the whole thing was shorthand for:
"cosA ~ 1 + (A^2)/2, where A is a very small angle (length, in radians), and the same for B and C".
Ulysees said:I guess some approximation of the expansion of cos might yield the pythagorean theoreom.
But I'm pondering, what are we doing here, we're mapping an abstract 2D curved space into ordinary euclidean space. General relativity is doing something analogous?
Could it be that a 3D or 4D curved space is just a mathematical trick, and in fact we can match experimental measurements with euclidean geometry too and the right formulation of relativity's equations?
Ulysees said:Can someone tell me, is it possible to match experimental measurements explained with GR but without including the concept of curved space and instead using relativistic equations in euclidean space?
MeJennifer said:The term Euclidean is, unfortunately, used for two distinct things, one refers to the metric signature and the other to the curvature of a space.
One can say unambiguously that any space that has an indefinite or a definite negative metric signature is not Euclidean even if that space is flat. Also any space that has a definite positive metric signature and is flat is Euclidean. However a space that has a definite positive metric signature and is not flat is sometimes also called Euclidean.
experimental measurements involving triangles cannot match a Euclidean theory
A non-euclidean space is a mathematical space that does not follow the rules and principles of Euclidean geometry, which is the study of points, lines, and angles in a flat, two-dimensional space.
In a non-euclidean space, the Pythagorean theorem does not hold true. This is because the Pythagorean theorem is based on the idea that the shortest distance between two points is a straight line, which is only true in Euclidean spaces. In non-euclidean spaces, the shortest distance between two points can be curved or even infinite.
Some examples of non-euclidean spaces include spherical geometry, which is the geometry of the Earth's surface, and hyperbolic geometry, which is the geometry of saddle-shaped surfaces. These spaces have different rules and principles compared to Euclidean geometry, leading to different measurements and calculations.
The concept of curvature is essential in understanding the Pythagorean theorem in non-euclidean spaces. In Euclidean spaces, the curvature is zero, and the Pythagorean theorem holds true. However, in non-euclidean spaces, the curvature is not zero, and thus the Pythagorean theorem does not apply.
Studying the Pythagorean theorem in non-euclidean spaces allows us to better understand the limitations of Euclidean geometry and the importance of considering different types of spaces in mathematical and scientific studies. It also has practical applications in fields such as astronomy, where non-euclidean spaces are used to calculate distances and measurements in the curved space of the universe.