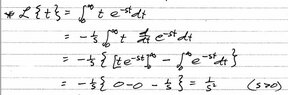nacho-man
- 166
- 0
Please refer to the attached image.
My lecturer seems to have re-written $e^{-st}$ as $\frac{d}{dt}e^{-st}$ and taken out the $(-\frac{1}{s}$ which I do see is equivalent, but i am unsure how he goes from there onwards.
Although, e is the derivative of itself. how does he split the integral into two, despite there being a multiplication of the terms?
My lecturer seems to have re-written $e^{-st}$ as $\frac{d}{dt}e^{-st}$ and taken out the $(-\frac{1}{s}$ which I do see is equivalent, but i am unsure how he goes from there onwards.
Although, e is the derivative of itself. how does he split the integral into two, despite there being a multiplication of the terms?