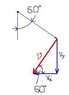
SUMMARY
The average velocity vector of a clock's minute hand, which is 5.5 cm long, during the interval from the hour to 20 minutes past the hour is calculated using the formula v = r x ω. The minute hand moves 120 degrees, or 1/3 of a circle, in this time frame. The angular velocity (ω) is determined to be 2π/60 radians per minute. The resulting velocity components are expressed as v = vxi + vyj, where vx = -v*cos(60°) and vy = -v*sin(60°).
PREREQUISITES
- Understanding of angular velocity and linear velocity concepts
- Familiarity with trigonometric functions (sine and cosine)
- Knowledge of vector notation in physics
- Basic geometry involving isosceles triangles
NEXT STEPS
- Study the relationship between linear and angular velocity in circular motion
- Learn how to apply trigonometric functions to solve vector problems
- Explore the concept of angular displacement and its applications
- Investigate the use of vector components in physics problems
USEFUL FOR
Students and professionals in physics, mathematics, and engineering who are interested in understanding circular motion and vector analysis.