xdrgnh
- 415
- 0
I'm trying to construct a Fisher Forecast for the upcoming S4 CMB survey. I don't understand
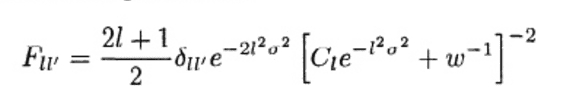
what the C_l is in this formula. It is H(z) and the Angular Distance? Or is it some covariance matrix and if it is a covariance matrix how do I calculate it considering the experiment hasn't been done yet?
In the end I want to calculate this
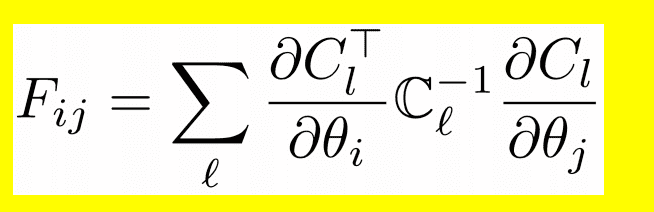
All help will be appreciated thanks.
what the C_l is in this formula. It is H(z) and the Angular Distance? Or is it some covariance matrix and if it is a covariance matrix how do I calculate it considering the experiment hasn't been done yet?
In the end I want to calculate this
All help will be appreciated thanks.