What is the derivation of the second equation for area velocity?

[Shreya]

Homework Statement

I want to understand the second equation for Areal velocity as given below.

Relevant Equations

Refer below.

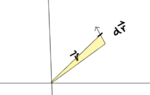
I think I understand how the first equation comes about.

In $dt$ the particle travels by $dr$, I considered it as a triangle with altitude $r$ and base $dr$. On dividing the area travelled in $dt$ by $dt$ we get the above equation.
A similar argument can be applied to $\frac 1 2 \rho^2 \frac {d\phi} {dt}$ as $\rho$ is same as r and $\rho \frac {d\phi} {dt}$ is same as $\frac {dr} {dt}$

But, I am not able to understand the 2nd equation. I can provide a similar argument for $xv_y$ but can,t seem to reason any further.
Please be kind to help.

 

[pasmith]

The unsigned area swept out in time $\delta t$ is approximately $$|\delta S| \approx \tfrac12 \|\mathbf{r} \times (\mathbf{r} + \mathbf{v}\delta t)\| = \tfrac12 \|\mathbf{r} \times \mathbf{v}\| |\delta t|.$$ This is because the magnitude of the cross-product gives the area of the parallelogram bounded by $\mathbf{r}$ and $\mathbf{r} + \mathbf{v} \delta t$, and the area swept out is approximately the area of a triangle which is one half of the parallelogram. Dividing by $\delta t$ and taking the limit $\delta t \to 0$ gives $$\left|\frac{dS}{dt}\right| = \tfrac12 \|\mathbf{r} \times \mathbf{v}\|.$$ This is essentially the derivation of the first formula.

To derive the second, in the case of motion in the $(x,y,0)$ plane we can calculate $\frac12\|\mathbf{r} \times \mathbf{v}\|$ either in cartesians or in plane polars using the standard formulae $$\begin{split} \mathbf{r} &= r\mathbf{e}_r(\theta) \\ \mathbf{v} &= \dot r \mathbf{e}_r(\theta) + r\dot \theta \mathbf{e}_{\theta}(\theta) \end{split}$$ where $$\mathbf{e}_r(\theta) \times \mathbf{e}_\theta(\theta) \equiv \mathbf{e}_z.$$ We can then adopt the convention that $S$ increases in the direction of increasing $\theta$ to remove the absolute value signs.

 

[Shreya]

To derive the second, in the case of motion in the (x,y,0) plane we can calculate 12‖r×v‖ either in cartesians or in plane polars using the standard formulae r=rer(θ)v=r˙er(θ)+rθ˙eθ(θ) where er(θ)×eθ(θ)≡ez. We can then adopt the convention that S increases in the direction of increasing θ to remove the absolute value signs.

Thank You so much @pasmith !
$\vec r = x \hat i + y \hat j$
$\vec v = v_x \hat i + v_y \hat j$

$\vec r \times \vec v = (x v_y - y v_x) \hat k$
$\frac {dS} {dt} = \frac 1 2 (xv_y-yv_x)$
Is the above right?