What is the electrical equivalent circuit for this interaction?

[mikejm]

A textbook gives an example of an ideal mass striking an ideal string here:

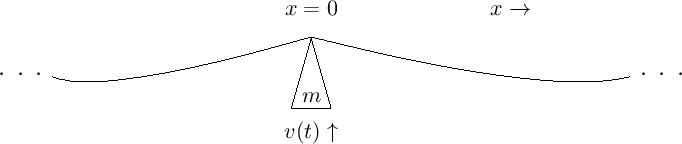
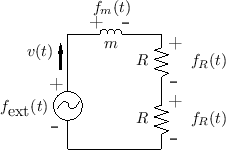
This is drawn as an equivalent electrical circuit as follows, where each R represents one of the two string segments the mass interacts with (ie. the string segment to the left of the mass and the string segment to the right):

A piano hammer is imagined slightly differently as a mass driving a damped spring against the string here (where the damping is roughly 0):

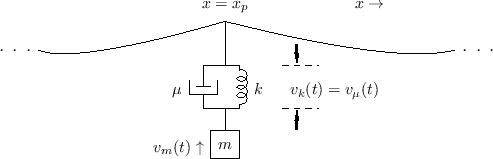
They state: "The impedance of this plucking system, as seen by the string, is the parallel combination of the mass impedance ms and the damped spring impedance mu + k/s. The damper mu and spring k/s are formally in series."

I am wondering how to draw the equivalent electrical circuit for this interaction. I am trying to figure out how to write equations for the forces and velocities of a hammer modeled in this way but I think I need the diagram first.

Here is my best guess. I put the damper (which is u=0) and spring in series, and their combination in parallel to the mass. I am uncertain of the + or - directions for the damper and spring:

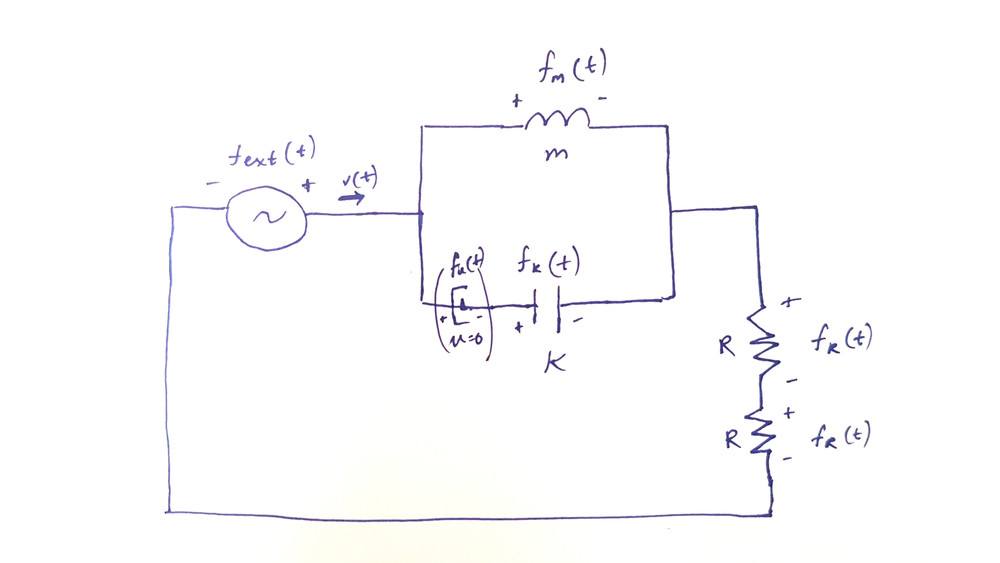
In the first case of the mass striking a string, because all the elements were in series, I believe the sum of forces (voltages) for the elements had to equal zero (Fm(t) + Fr(t) + Fr(t) + Fext(t) = 0). What would that equation of forces look like for this circuit?

I'm guessing it would be something like an equation system based on the parallel sections:

Fm(t)+Fr(t)+Fr(t)+Fext(t)=0
Fk(t)+Fr(t)+Fr(t)+Fext(t)=0
Fm(t)=Fk(t)

Is that correct?

 

[tech99]

In the first case, I should have thought that the moving mass is equivalent to a lossless inductor with a short circuit in which a direct current is flowing. When it strikes the string, a switch, having the two resistors across it in parallel, is opened. It becomes an L-R ciruit having a time constant of 2L/R.
In the second case, it looks as if the initial mass (inductance) has a damping resistance in parallel to it. With DC circulating current, there is no voltage across the damping resistor, but when the switch opens, the forward EMF is developed across the damping resistor, so dissipating energy.
In a practical case, I suspect that the damping is chosen to minimise the noise of the hammer; in other words, at higher frequencies than the fundamental of the string.
These cases look rather like a spark transmitter, where a capacitor is charged by DC and then connected to an inductor and a resistive load, so that damped oscillations occur.

 

[Dr.D]

Trying to draw such equivalences is asking for trouble. It is far better to work the original problem as given than to try to trade it for another problem.