What is the internal radius of the optical fibre

[Ajaroy]

Homework Statement

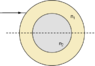
A Capillary tube is made of glass of refractive index n₁ . The outer radius of the tube is R.The tube is filled with a liquid of refractive index n₂ < n₁ .what should be the minimum internal radius of the tube so that any ray that hits the tube would enter the liquid

Homework Equations

The Attempt at a Solution

I know that in an optical fibre they are core and cladding.it operates by principle of total internal reflection.i have calculated maximum incident angle possible
As i = arcsin √n₁²
-n₂²

How to get terms in terms of R and should we consider any size approximations as it is a capillary tube is what I can't understand.
If we should consider approximations then how?Please help me

 

[kuruman]

I don't think this question is related to an optical fiber with cladding. Consider the drawing that shows a ray coming in from the outside. A typical ray is shown incident on the capillary. The question is how small the inner radius can be so that all the rays incident on the outside enter the inner tube. Draw a neat ray diagram of the path that the ray shown follows and write some equations down. Hint: A useful parameter is the vertical distance between the ray and the dotted line.

 

[Merlin3189]

A Capillary tube is made of glass of refractive index n₁ . The outer radius of the tube is R.The tube is filled with a liquid of refractive index n₂ < n₁ .
what should be the minimum internal radius of the tube so that any ray that hits the tube would enter the liquid

Have you considered the possibility that this is not about an optic fibre? It sounds to me as if the light might be striking perpendicular to the axis of the tube. Otherwise I can't see any reason why a paraxial ray should ever enter the liquid.

Try drawing a diagram.