Up_Creek
- 18
- 0
Ok
here's the question;
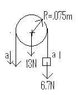
"You pull downward with a force of 25N on a rope that passes over a disk-shaped pulley of mass 1.3 kg and radius 0.075m. The other end of the rope is attached to a .67-kg mass. (a) Us the tension in the rope the same on both sides of the pulley? If not, which side has the largest tension? (b) Find the tension in the rope on both sides of the pulley.
(c) Find the linear acceleration of the .67kg mass.
Ok, we're using g=10 m/s so the pulley is 13N and the mass is 6.7N.
I've gotten all the forces drawn in but I'm kind of sketchy about how to get the answer. I know I need to combine several equations to find t, tension.
So in total I have this attached image here.
The steps I know I need are as follows
1.) Draw a picture
2.) isolate bodies
3.) draw in forces
4.) resolve forces
I know i'll need to use F=ma. I'm assuming that hopefully I can re-work that so I get a=F/m? Also, as (c) was the only question assigned, do I need to do (a) and (b) to get (c)?
a rough outline of what I think
Since the 25N force is greater than the 6.7N mass, the pulley will accelerate counter-clockwise (or 'out' according to the right hand rule, not sure why that's important, or even if it is) So i'll take counter-clockwise to be positive. Tension must be down, since rope cannot push. Obviously the tension is different on both sides of the pulley, or they wouldn't word the question like that, and the force on the 25N side would create more tension on that side too, right?
Anyway, I need to find the linear acceleration of the 6.7N mass. Linear acceleration I think would be acceleration in the y direction, right?
Jordan Veale
here's the question;
"You pull downward with a force of 25N on a rope that passes over a disk-shaped pulley of mass 1.3 kg and radius 0.075m. The other end of the rope is attached to a .67-kg mass. (a) Us the tension in the rope the same on both sides of the pulley? If not, which side has the largest tension? (b) Find the tension in the rope on both sides of the pulley.
(c) Find the linear acceleration of the .67kg mass.
Ok, we're using g=10 m/s so the pulley is 13N and the mass is 6.7N.
I've gotten all the forces drawn in but I'm kind of sketchy about how to get the answer. I know I need to combine several equations to find t, tension.
So in total I have this attached image here.
The steps I know I need are as follows
1.) Draw a picture
2.) isolate bodies
3.) draw in forces
4.) resolve forces
I know i'll need to use F=ma. I'm assuming that hopefully I can re-work that so I get a=F/m? Also, as (c) was the only question assigned, do I need to do (a) and (b) to get (c)?
a rough outline of what I think
Since the 25N force is greater than the 6.7N mass, the pulley will accelerate counter-clockwise (or 'out' according to the right hand rule, not sure why that's important, or even if it is) So i'll take counter-clockwise to be positive. Tension must be down, since rope cannot push. Obviously the tension is different on both sides of the pulley, or they wouldn't word the question like that, and the force on the 25N side would create more tension on that side too, right?
Anyway, I need to find the linear acceleration of the 6.7N mass. Linear acceleration I think would be acceleration in the y direction, right?
Jordan Veale
Attachments
Last edited: