Discussion Overview
The discussion revolves around the interpretation of the notation "+:0" encountered while using the HP 50g emulator to compute a limit involving exponential functions. Participants explore its meaning in the context of limits and the behavior of the calculator.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- One participant questions the meaning of "+:0" in the context of their limit computation.
- Another participant suggests estimating the answer and analyzing the terms separately.
- Multiple participants recommend consulting the HP 50g manual for clarification on "+:0".
- One participant proposes that "+:0" indicates approaching the limit from the right, while "-:0" would indicate approaching from the left.
- Another participant challenges this interpretation, noting that the limit is as x approaches infinity, and asserts that the limit itself is infinity.
- Some participants reference specific pages in the manual where related information can be found, but express uncertainty about the exact notation "+:0".
- One participant mentions that the HP 50g emulator may produce incorrect results due to stack overflow issues at certain limits.
Areas of Agreement / Disagreement
Participants express differing interpretations of the notation "+:0" and whether it is relevant in the context of limits approaching infinity. There is no consensus on the meaning of the notation, and the discussion remains unresolved regarding its implications.
Contextual Notes
There are references to potential limitations in the HP 50g emulator's handling of limits, particularly concerning stack overflow at extreme values, which may affect the accuracy of results.
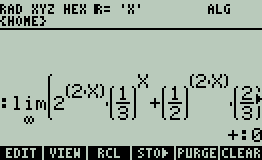 What is the meaning of +:0 ?
What is the meaning of +:0 ?