What Is the Non-Deformed Length of a Spring Between Two Linked Bodies?

[inv4lid]

Homework Statement

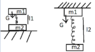
two linked are attached to each other with a spring. If the second body is placed on a fixed support, the length of the spring is 5 cm. If we fix the first body as in the picture, the length of the spring becomes 15cm. Determine the length of the spring in the non-deformed state.

m1 = 1 kg;
m2 = 4kg;
l1 = 5cm;
l2 = 15cm;

Homework Equations

This time i have really no idea. The m1 pushes the spring with a force of 10N and m2 should like respond with another force? Quite don't get it.

The Attempt at a Solution

Any help would be greatly appreciated.

 

[PeroK]

I suggest using Hooke's law.

 

[inv4lid]

I suggest using Hooke's law.

10 N = kΔL?
ΔL₁ = L₁ - L₀ from there
L₀ = -ΔL₁+L₁ -> L₀ = -ΔL₁+5
ΔL₂ = L₂-L₀ from there
L₀ = -ΔL₂+L2 -> L₀ = -ΔL₂+15
Quite still don't get it.

 

[PeroK]

10 N = kΔL?
ΔL₁ = L₁ - L₀ from there
L₀ = -ΔL1+L1 -> L0 = -ΔL₁+5
ΔL₂ = L₂-L₀ from there
L₀ = -ΔL2+L2 -> L0 = -ΔL₂+15
Quite still don't get it.

If we take the first case with the mass $m_1$. Let $L$ be the natural length of the spring and $x_1 > 0$ be the contraction due to $m_1$. Then, by Hooke's law:

$m_1g = kx_1$

Where $k$ is the (unknown) sprong constant.

Does that get you started?

 

[inv4lid]

If we take the first case with the mass $m_1$. Let $L$ be the natural length of the spring and $x_1 > 0$ be the contraction due to $m_1$. Then, by Hooke's law:

$m_1g = kx_1$

Where $k$ is the (unknown) sprong constant.

Does that get you started?

What is x?
I assume it's a different writing form of ΔL? Ok.
Sorry, but i have already tried that above.
mg (which is 10N) = kx, where both k & x are unknown

 

[PeroK]

What is x?

$x_1$ is the distance that the spring is compressed from its natural length under the weight of $m_1$.

 

[PeroK]

What is x?
I assume it's a different writing form of ΔL? Ok.
Sorry, but i have already tried that above.
mg (which is 10N) = kx, where both k & x are unknown

Yes, I forgot you had used $\Delta L_1$.

It doesn't matter how many unknowns you have at this stage. The trick is keep going with the next equation and hope that you can get rid of the unknowns at some stage.

 

[inv4lid]

Yes, I forgot you had used $\Delta L_1$.

It doesn't matter how many unknowns you have at this stage. The trick is keep going with the next equation and hope that you can get rid of the unknowns at some stage.

A question there: why do we need m2 there if it doesn't influence the object?

 

[PeroK]

A question there: why do we need m2 there if it doesn't influence the object?

We don't. I think the premise is that they are joined together. The mass of $m_2$ doesn't affect the first scenario, nor does $m_1$ affect the second.

You might also ask how they managed to attach $m_1$ to the ceiling, but I wouldn't worry about that either.

 

[inv4lid]

Okay.
m₁g = k(x₁-x₀)
m₁g = k(x₂-x₀)
->
10 = k(5-x₀)
10 = k(15-x₀) that's though quite non-sense

 

[PeroK]

Okay.
m₁g = k(x₀-x₁)
m₁g = k(x₀-x₂)
->
10 = k(x₀-5)
10 = k(x₀-15) that's though quite non-sense

In post #4 I had:

$m_1g = kx_1$

That seemed the simplest approach. My thinking was: the spring is being compressed by a certain amount. Let's call that $x_1$.

But, if you are going to use:

$m_1g = k(x_0 - x_1)$

Then you have to be careful about what $x_0$ and $x_1$ are.

In your second equation things have gone wrong. You've still got $10$ for the force, which can't be right. And, you've got negative numbers creeping in.

Anyway, you need to fix those equations. We can stick with your notation, but you need to be careful about how you are defining things.

 

[inv4lid]

In post #4 I had:

$m_1g = kx_1$

That seemed the simplest approach. My thinking was: the spring is being compressed by a certain amount. Let's call that $x_1$.

But, if you are going to use:

$m_1g = k(x_0 - x_1)$

Then you have to be careful about what $x_0$ and $x_1$ are. $x_1$ can't be "5" here.

In your second equation things have gone wrong. You've still got $10$ for the force, which can't be right. And, you've got negative numbers creeping in.

Anyway, you need to fix those equations. We can stick with your notation, but you need to be careful about how you are defining things.

Okay. Ty for everything, going to solve it.