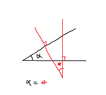
What is the proof for angle equality?

  • Context: MHB 
  • Thread starter Thread starter paulmdrdo1
  • Start date Start date
  • Tags Tags
    Angle Proof
Click For Summary
SUMMARY

The proof for angle equality, specifically regarding opposite angles formed by intersecting lines, is established by the theorem stating that when two lines intersect, the opposite angles are equal. This fundamental geometric principle confirms that angles formed by the intersection of two lines are congruent. Additionally, it is noted that angles with mutually perpendicular sides are also equal, reinforcing the concept of angle equality in geometry.

PREREQUISITES
  • Understanding of basic geometric principles
  • Familiarity with angle relationships in intersecting lines
  • Knowledge of theorems related to perpendicular lines
  • Basic trigonometry concepts
NEXT STEPS
  • Study the properties of intersecting lines and angle relationships
  • Review the theorem on angles with mutually perpendicular sides
  • Explore proofs related to angle congruence in geometry
  • Investigate applications of angle equality in trigonometry
USEFUL FOR

Students studying geometry, educators teaching angle relationships, and anyone interested in understanding the proofs behind angle equality in mathematics.

paulmdrdo1
Messages
382
Reaction score
0
I've been searching over the internet and geometry books for the proof of the relationship of these two angles but I couldn't find one. Can you tell me the "how" and "why" of their equality. thanks and regards!
 

Attachments

  • equal angles.png
    equal angles.png
    3.2 KB · Views: 92
Mathematics news on Phys.org
Use the fact that when two lines intersect, opposite angles are equal. The result then follows.
 
Check post #5.

http://mathhelpboards.com/trigonometry-12/equality-angles-11593.html

"There is a theorem saying that two angles whose sides are mutually perpendicular are equal. "
 

Similar threads

High School I've been trying to understand the proof for the binomial theorem
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Proof for interpolating polynomial and error approximation
  • · Replies 6 ·
Replies
6
Views
2K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Prove that solid angle of any closed surface is 4pi
  • · Replies 5 ·
Replies
5
Views
9K
Suggestions for HS geometry book (proofs)
  • · Replies 14 ·
Replies
14
Views
3K
High School What is the difference between the two sine rules for resultant vector?
  • · Replies 4 ·
Replies
4
Views
2K
MHB Proving the Angle-Angle-Side Theorem
  • · Replies 1 ·
Replies
1
Views
2K
Graduate How did Saccheri prove Euclid's Fifth Postulate?
  • · Replies 6 ·
Replies
6
Views
3K
Undergrad Question about Euclid's parallel postulate (5th postulate).
  • · Replies 16 ·
Replies
16
Views
4K
MHB Find the Bearing from A to C & Angle B: Solve Here
  • · Replies 3 ·
Replies
3
Views
2K