- #1
Master1022
- 590
- 116
- TL;DR
- What is the purpose of the Prandtl mixing method and what does it mean?
Hi,
I was recently learning about turbulent boundary layers and came across the 'Prandtl mixing length'. I am struggling to understand what the concept is and what its purpose is. I would appreciate any help or guidance of where I can look to gain a better understanding.
The information I currently know is below.
The turbulent 2D boundary layer momentum equation is given by:
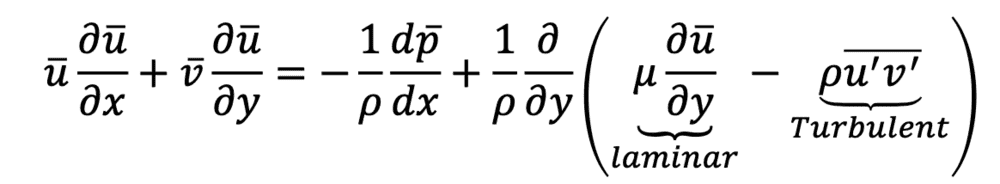
Then we can define an eddy viscosity \epsilon_{M} such that:
\tau_{turbulent} = - \rho \overline{u' v'} = \rho \epsilon_{M} \frac{du}{dy}
The cyclic motion of a turbulent packet of fluid results in a turbulent shear stress. Therefore, we seek some model to relate this motion to eddy viscosity. Prandtl postulated that the turbulent fluctuation u' is proportional to the time average of the absolute value of these fluctuations, thus giving:
u' = l' \frac{du}{dy}
This distance l is called Prandtl’s mixing length. Also the idea that u' would be the same order of magnitude as v′ (assumption only valid for isotropic turbulence). Giving:
\tau_{turbulent} = - \rho \overline{u' v'} = \rho \epsilon_{M} \frac{du}{dy} = \rho l^2 \left( \frac{du}{dy} \right)^2
The eddy viscosity varies through the boundary layer. Prandtl’s hypothesis was that the mixing length is proportional to the distance from the wall, l = ky where k is a constant and also the shear stress is uniform and approximately equal to the value at the wall in the region close to the wall, \tau_t = \tau_w. This leads to an expression for the shear stress
\tau_t = \rho k^2 y^2 \left( \frac{du}{dy} \right)^2
y is the upper bound of l since mixing length cannot be greater than the distance from the wall by our definition. Taking the square root and integrating gives:
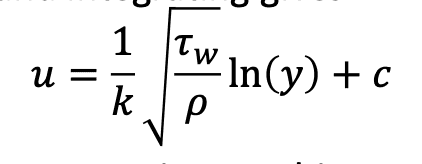That is the text that I have on the topic. After reading this, I am not completely sure what the purpose of this concept is.
Thanks in advance.
I was recently learning about turbulent boundary layers and came across the 'Prandtl mixing length'. I am struggling to understand what the concept is and what its purpose is. I would appreciate any help or guidance of where I can look to gain a better understanding.
The information I currently know is below.
The turbulent 2D boundary layer momentum equation is given by:
Then we can define an eddy viscosity \epsilon_{M} such that:
\tau_{turbulent} = - \rho \overline{u' v'} = \rho \epsilon_{M} \frac{du}{dy}
The cyclic motion of a turbulent packet of fluid results in a turbulent shear stress. Therefore, we seek some model to relate this motion to eddy viscosity. Prandtl postulated that the turbulent fluctuation u' is proportional to the time average of the absolute value of these fluctuations, thus giving:
u' = l' \frac{du}{dy}
This distance l is called Prandtl’s mixing length. Also the idea that u' would be the same order of magnitude as v′ (assumption only valid for isotropic turbulence). Giving:
\tau_{turbulent} = - \rho \overline{u' v'} = \rho \epsilon_{M} \frac{du}{dy} = \rho l^2 \left( \frac{du}{dy} \right)^2
The eddy viscosity varies through the boundary layer. Prandtl’s hypothesis was that the mixing length is proportional to the distance from the wall, l = ky where k is a constant and also the shear stress is uniform and approximately equal to the value at the wall in the region close to the wall, \tau_t = \tau_w. This leads to an expression for the shear stress
\tau_t = \rho k^2 y^2 \left( \frac{du}{dy} \right)^2
y is the upper bound of l since mixing length cannot be greater than the distance from the wall by our definition. Taking the square root and integrating gives:
Thanks in advance.