What is the relationship between a vector and a plane in terms of parallelism?
Click For Summary
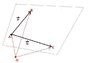
The discussion centers on understanding the relationship between vectors and planes, particularly regarding parallelism. It explains that two intersecting lines define a plane, with vectors b and c representing these lines. The vectors lie within the same plane, and their parallelism to the plane is clarified through a visual analogy involving a sheet of paper. By lifting the paper, one can visualize how the vectors relate to the plane and the points within it. This explanation helps clarify the concept for those struggling with the geometric representation.
Similar threads
- · Replies 6 ·
- · Replies 8 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 2 ·
- · Replies 9 ·
- · Replies 2 ·
- · Replies 5 ·
![DSC_0001~8~2[1].jpg](/data/attachments/53/53885-6609e8ddcfebb400cedbdf58bdc5773a.jpg?hash=Zgno3c_rtA)