Calculating the distance from a point to a plane

[Darkmisc]

Homework Statement

What is the distance from r*(2i -j -2k) = 7 to the point (1, 1, -1)?

Relevant Equations

d=|PQ*n|

Hi everyone

I have worked solutions to the question, but I don't fully understand what they are doing and I get a different answer.

I used d=|PQ*n| and chose (0, 0, -7/2) as a point on the plane. I got that point by letting i and j = 0.

Since P = (1, 1, -1), PQ = (-1, -1, -5/2).

The unit vector of the normal works out to be (1/3)(2i -j -2k)

So d = |(-1, -1, -5/2)*(1/3)*(2, -1, -2)| = 4/3.

These are the worked solutions.

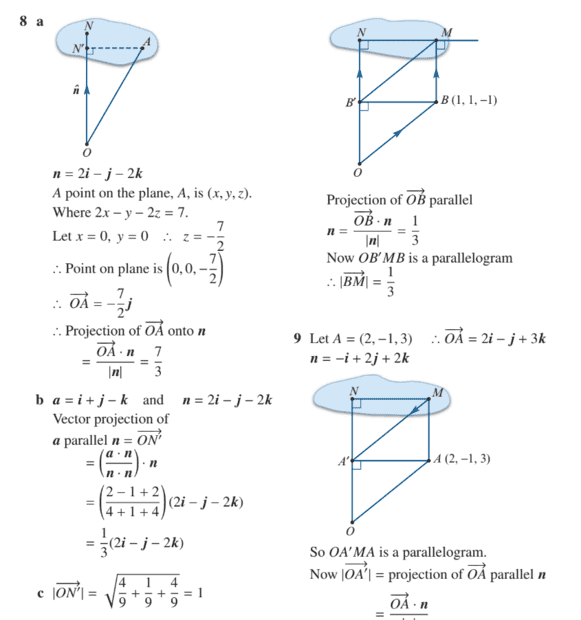
I understand the general logic behind it and can accept that OB' = BM. However, I don't understand how they know M is a point on the plane. Is it not possible for OB'MB to form a parallelogram without M touching the plane?Thanks

 

[DrClaude]

I understand the general logic behind it and can accept that OB' = BM. However, I don't understand how they know M is a point on the plane. Is it not possible for OB'MB to form a parallelogram without M touching the plane?

You define M to be the point on the plane closest to B.

That said, the solution is full of mistakes. First, it should be $\overrightarrow{OA} = \frac{7}{2} \mathbf{k}$.

Then, I get
$$
\frac{\overrightarrow{OB} \cdot \mathbf{n}}{|\mathbf{n}|} = 1,
$$
not $1/3$, such that $|\overrightarrow{OB'}| = 1$. Since $|\overrightarrow{ON}| = 7/3$, this means that $|\overrightarrow{B'N}| = 4/3$. I then take $|\overrightarrow{BM}| = |\overrightarrow{B'N}| = 4/3$, so I get the same answer as you did (and I like your approach better). I'm not sure I get the parallelogram either.