What is the Role of Torque in Holding a Sphere Against a Wall?

[vibha_ganji]

Homework Statement

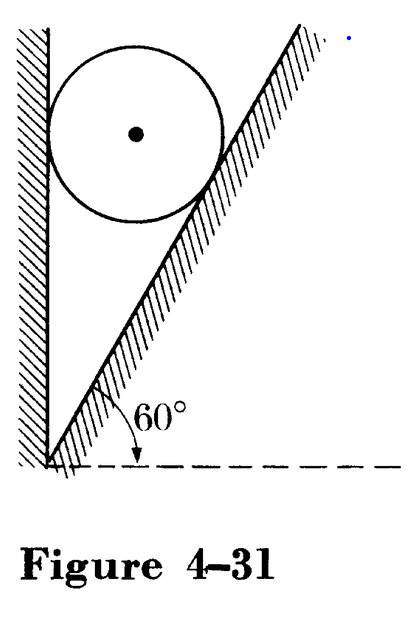
A sphere (Fig. 4-31) weighing 50 lbf is leaning against a smooth wall, held there by a smooth inclined plane that forms a 60° angle with the horizontal. Calculate the reaction of the wall and the plane on the sphere. Source: Alonso and Finn Volume 1

Relevant Equations

W = mg
Tau (torque) = r times F

I’m pretty sure that the force on the sphere by the wall and plane has to equal mg so the sum of the normal force is steered by the wall and plane has to equal mg. I’m not sure where to go after this. Is mg the answer or is there something I’m missing?Here is Fig: 4-31:

 

[Delta2]

The vector sum of the force from the wall and the force from the inclined plane is indeed equal (and opposite in order to be more precise since we have vectors) to the vector of weight of the sphere. But the problem statement asks you to calculate the above individual forces not their vector sum.

Make an FBD of the sphere. Choose a coordinate system such that y-axis is the direction of the wall and the x-axis is vertical to it (the horizontal). Analyze all the forces (especially the force of normal from the inclined plane) to x and y components. Finally since the sphere is in equilibrium, apply the static conditions that the algebraic sum all of the x components (of the forces in play) is zero, and also that the algebraic sum of all of the y components is zero as well.

 

[jedishrfu]

FBD is an abbreviation for Free Body Diagram.

 

[haruspex]

such that y-axis is the direction of the wall and the x-axis is vertical to it (the horizontal).

You meant "such that y-axis is the direction of the wall (vertical) and the x-axis is normal to it (the horizontal)", right?

 

[Delta2]

You meant "such that y-axis is the direction of the wall (vertical) and the x-axis is normal to it (the horizontal)", right?

yes

 

[hmmm27]

Tau (torque) = r times F

Do you need this formula ?