What is this formula being used to calculate drag force?

[grandpa2390]

Homework Statement

I'm writing a program to plot the trajectory of a baseball. the formula is given to me by the book, but I'm not sure what it means.

Homework Equations

The Attempt at a Solution

I am given that v_d = 35 m/s and delta = 5 m/s

what is v? as in what does it represent? is it the velocity? is it something else?
I use it in a formula to calculate the drag force.

dragForce = Bm * sqrt(initialVelocityX^2 + initialVelocityY^2)

my entire program so far is this

close all
clear all
clc

%define Variables and Matrices
timeStep = .25
initialPositionX = 0
initialPositionY = 0
initialVelocity = 110*0.44704 %mph to m/s
positionX = zeros(1,50);
positionY = zeros(1,50);
positionX(1) = initialPositionX;
positionY(1) = initialPositionY;
theta = 35 * 0.0174533 %degrees to radians
initialVelocityX = initialVelocity * cos(theta)
initialVelocityY = initialVelocity * sin(theta)
vd = 35 %m/s
delta = 5 %m/s

Bm = .0039 + (.0058)/(1+exp((initialVelocity-vd)/delta)) %B2/m

for i = 2:1000
    positionX(i) = positionX(i-1) + initialVelocityX * timeStep
    positionY(i) = positionY(i-1) + initialVelocityY * timeStep
    dragForce = Bm * sqrt(initialVelocityX^2 + initialVelocityY^2)
    initialVelocityY = initialVelocityY - (9.8 * timeStep) - (dragForce * initialVelocityY * timeStep)
    initialVelocityX = initialVelocityX - (dragForce * initialVelocityX * timeStep)
    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2) 
    %Bm = .0039 + (.0058)/(1+exp((initialVelocity-vd)/delta))
    if positionY(i) <= 0 
        break
    end
end

%a = -positionY(i) / positionY(i-1)
%positionX(i) = (positionX(i) + (a * positionX(i-1))) / (1 + a)
%positionY(i) = 0

%%Plots
figure(1)
hold on
box on
plot(positionX,positionY,'-k')
set(gca,'Xtick',linspace(0,150,4),'fontsize',18,'Ytick',linspace(0,50,6))
set(gcf,'Color','w');
set(gcf,'Resize','on');

ylim([0 30])
xlim([0 150])
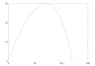
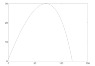
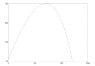
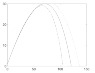
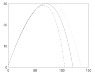
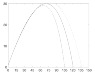
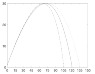
hold off

You'll notice the line of code right before the For loop is what I am speaking of. You can also see in my for loop to lines of code commented out. Not knowing what v is, I thought maybe it is the current velocity and that perhaps Bm and then the drag force should change as the velocity changed. It brought my plot closer to where it ought to be (a peak at x= 70 and y=30 and a landing point at about x=120)
But since it didn't solve the problem, I commented it out and came here hoping for a better understanding of what that formula is asking. because in the cannonball program I just did, Bm was given as a constant. Of course air density wasn't included (as the book says it is in this function) and I think the cannonball was smooth (which a baseball is not).

so maybe I am kind of correct and it should change with velocity. The book does have chart showing the change in drag coefficient vs velocity for rough, smooth, and normal baseball.

I don't know. Is that v the current velocity. should Bm be recalculated with every change in velocity? Did I make dumb typos that have resulted in my program breaking that only fresh eyes can spot? :)

 

[haruspex]

Yes, v is the current velocity. The commented out lines should be reinstated.

since it didn't solve the problem,

Didn't solve what problem?

 

[willem2]

initialVelocityY = initialVelocityY - (9.8 * timeStep) - (dragForce * initialVelocityY * timeStep)
initialVelocityX = initialVelocityX - (dragForce * initialVelocityX * timeStep)

I don't see why you multiply the dragforce here with InitialVelocityX or InitialvelocityY. You didn't do that with gravity.

 

[grandpa2390]

I don't see why you multiply the dragforce here with InitialVelocityX or InitialvelocityY. You didn't do that with gravity.

well, first, I copied this code from code the author wrote for a cannonball problem. and that's what he did. But it is my understanding that we are looking at a kinematic equation V = Vo + a*dt which is: Current Velocity = initial Velocity + (-drag force * initialVelocity * dt).

a = dV/dt. due to gravity, dV/dt = -9.8 m/s^2 ... for factoring in he drag force, dV/dt = drag Force * velocity.

I'm not saying that I 100% understand this. it is just what the author says:

I myself wondered why I couldn't just plug vy in line 5 into vy in. line 3. likewise with vx. why would I have to have 2 separate steps. but no matter what I do, whenever I try to reduce steps by putting vy into the x(i) formula. I get a completely different graph. and not a better one.

I'll try multiplying 9.8 by the drag. see what happens :)

edit: so I tried it, but the drag coefficient is a fraction, and the ball just ended up shooting out into space. it is just my guess, but drag coefficient times velocity is a dV/dt. I'll have to check the units, we are calculating how drag changes the velocity over the course of dt. how the acceleration due to gravity changes the velocity. and then factoring in those changes.

edit2: so dragForce = bm * velocity. so dragForce should have units of m/s. so v * v * dt... m^2 / s... that doesn't seem right. it's the formula given by the book though. dragForce should have units of s^-2 ... if you have any ideas, I welcome them.

edit3: went through my notes and my instructor said the same thing.
the actual formula is ((B*v*v_x)dt)/m
bm = B/m
dragForce = bm*v
and the change in velocity due to drag is dragForce*v_x*dt

 

[grandpa2390]

Yes, v is the current velocity. The commented out lines should be reinstated.

Didn't solve what problem?

I am trying to get this

right now I am working on just the line with no wind. Just the force of drag. I am close, but something is wrong because the ball travels too high and lands a bit too far.

If I shift around the code to this:

%x() and y() are the positions of the projectile

%dt = time step

%v_init = initial speed

%theta = launch angle

%B_m = proportional to drag force = B2/m

close all

clear all

clc
%define Variables and Matrices

timeStep = .25

initialPositionX = 0

initialPositionY = 1

initialVelocity = 110*0.44704 %mph to m/s

positionX = zeros(1,50);

positionY = zeros(1,50);

positionX(1) = initialPositionX;

positionY(1) = initialPositionY;

theta = 35 * 0.0174533 %degrees to radians

initialVelocityX = initialVelocity * cos(theta)

initialVelocityY = initialVelocity * sin(theta)

vd = 35 %m/s

delta = 5 %m/s

gravity = -9.8
Bm = .0039 + (.0058)/(1+exp((initialVelocity-vd)/delta)) %B2/m
velocity = initialVelocity

velocityX = initialVelocityX

velocityY = initialVelocityY
for i = 2:1000

    %positionX(i) = positionX(i-1) + velocityX * timeStep

    %positionY(i) = positionY(i-1) + velocityY * timeStep 

    velocity = sqrt(velocityX^2 + velocityY^2)

    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))

    dragForce = Bm * velocity

    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)

    velocityX = velocityX - (dragForce * velocityX * timeStep)

    positionX(i) = positionX(i-1) + velocityX * timeStep

    positionY(i) = positionY(i-1) + velocityY * timeStep 

    %velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)

    %velocityX = velocityX - (dragForce * velocityX * timeStep)

    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)

    %positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep

    %positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep

    %Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))

    if positionY(i) <= 0 

        break

    end

end
%a = -positionY(i) / positionY(i-1)

%positionX(i) = (positionX(i) + (a * positionX(i-1))) / (1 + a)

%positionY(i) = 0
%%Plots

figure(1)

hold on

box on

plot(positionX,positionY,'-k')

set(gca,'Xtick',linspace(0,150,4),'fontsize',18,'Ytick',linspace(0,50,6))

set(gcf,'Color','w');

set(gcf,'Resize','on');
ylim([0 30])

xlim([0 150])

hold off
[/quote]

I was playing with it late last night. If you ask me why I changed the order of operation in the For loop, I'd have to look at it real closely. trying to figure out whether the position should be calculated before or after the velocity is recalculated.  According to the author, it should be before. but I was feeling a bit desperate, and had some "eureka" moments of things I might try. I even tried splitting the drag force into components. but that didn't work out very well. and it wasn't necessary for the cannonball problem.

 

[haruspex]

I don't see why you multiply the dragforce here with InitialVelocityX or InitialvelocityY. You didn't do that with gravity.

It is to obtain the component in that direction.
I would say the drag force is quadratic, F_d=kv². The vertical component is then $kv^2\frac{v_y}{v}=kvv_y$.

 

[haruspex]

something is wrong because the ball travels too high and lands a bit too far.

Have you tried reducing the timestep? If that changes the result noticeably it tells you it was too large.

 

[willem2]

I was playing with it late last night. If you ask me why I changed the order of operation in the For loop, I'd have to look at it real closely. trying to figure out whether the position should be calculated before or after the velocity is recalculated. According to the author, it should be before. but I was feeling a bit desperate, and had some "eureka" moments of things I might try. I even tried splitting the drag force into components. but that didn't work out very well. and it wasn't necessary for the cannonball problem.

I believe what you have now is correct.
The probem with the order of operations is one of the reasons why the euler method is not a very accurate integration method. Both ways of doing it give errors.
In one case you use:
x_t+dt = x_t + v_t dt
In the other case:
x_t+dt = x_t + v_t+dt dt
while you really need
x_t+dt = x_t + v_{average in time interval from t to t+dt} dt
The computations of y, vx and vy have the same problem. The largest error seems to come from the calculation of vx. You always use the old value of v in the drag calculation, which is always too high, so the calculated drag is always too large, and these errors accumulate in vx. The errors in the vy calculation on the way up get mostly canceled on the way down.
Reducing the step size will reduce the errors. A step size of 0.25 s is quite large, since the whole thing only takes 4 seconds or so. The true value is about 30% off using this timestep.

If you use
$$x_{t+dt} = x_t + \frac { v_{t+dt} + v_t } {2} dt$$ instead, this is known as the midpoint method. First you compute approximate new values of x, y, vx and vy as before, and then you do the calculations again using the average of the old and the new values.

 

[FactChecker]

The largest error seems to come from the calculation of vx. You always use the old value of v in the drag calculation, which is always too high, so the calculated drag is always too large, and these errors accumulate in vx.

This is good analysis, but he says that the ball goes too high and too far. That would indicate that his drag is too small. Something else is wrong.

 

[willem2]

This is good analysis, but he says that the ball goes too high and too far. That would indicate that his drag is too small. Something else is wrong.

It turns out I made an error in the drag equation that made my drag too high.With much less drag, the primary source of error is: x_t+dt = x_t + vx_t dt. This will tend to use values of vx that are too high, and x will get higher for larger values of dt.
with dt = 0.01, both the maximum altitude and the distance are the same as in the graph.

 

[haruspex]

with dt = 0.01

Yes, (see post #7) it is always a good idea to check whether reducing the timestep changes the answer - even if you do not have reason to suspect a problem.

 

[grandpa2390]

Have you tried reducing the timestep? If that changes the result noticeably it tells you it was too large.

that never crossed my mind...simple and it makes perfect sense.
Reducing it is getting me closer and closer.

 

[grandpa2390]

This is good analysis, but he says that the ball goes too high and too far. That would indicate that his drag is too small. Something else is wrong.

It turns out I made an error in the drag equation that made my drag too high.With much less drag, the primary source of error is: x_t+dt = x_t + vx_t dt. This will tend to use values of vx that are too high, and x will get higher for larger values of dt.
with dt = 0.01, both the maximum altitude and the distance are the same as in the graph.

actually, some of the changes I made in my program last night trying to fix my error produced a graph that was too low. Specifically, moving the calculation of position from the beginning of the loop to the end of the loop. Basically the two options @willem2 gave with subscripts. one results in a margin of error that is large and the other small, it seems :)
from:

    positionX(i) = positionX(i-1) + velocityX * timeStep
    positionY(i) = positionY(i-1) + velocityY * timeStep
    velocity = sqrt(velocityX^2 + velocityY^2)
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    dragForce = Bm * velocity
    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    velocityX = velocityX - (dragForce * velocityX * timeStep)
    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep

to

    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep
    velocity = sqrt(velocityX^2 + velocityY^2)
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    dragForce = Bm * velocity
    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    velocityX = velocityX - (dragForce * velocityX * timeStep)
    positionX(i) = positionX(i-1) + velocityX * timeStep
    positionY(i) = positionY(i-1) + velocityY * timeStep

changes whether the graph is too high or too low.

in either case, reducing the the time step to .01, I find is getting it much closer. I will try even lower numbers. It is important to my professor that it looks precisely like the graph. and even at .01, there is a noticeable bit of white space that says the the trajectory is going a tad higher or lower than y=30 :)

edit
at timeStep = .0025 :D

now for wind :)

 

[haruspex]

changes whether the graph is too high or too low.

You could compromise by taking the averages of the old and new velocities for calculating the position change.

 

[FactChecker]

actually, some of the changes I made in my program last night trying to fix my error produced a graph that was too low. Specifically, moving the calculation of position from the beginning of the loop to the end of the loop.

Because everything you calculated would actually happen continuously and instantly in the real world, there is no perfect order to put your calculations in. When the time step is smaller, your calculations are closer to the continuous situation, regardless of order, and the answers should get more accurate. Your original time step of dt=0.25 at an initial velocity of 35 m/s allowed a lot of motion (almost 10 meters) between calculations. That is too much motion for the accuracy you want. A calculation rate of 400 per second is not unreasonable. There are situations (like a car on the ground where the suspension spring compression depends on inches above the ground) where calculation rates of thousands per second are required. Advanced simulation tools can monitor how rapidly things are changing in the simulation of continuous processes and adjust the time step size appropriately as it progresses through simulated time.

 

[grandpa2390]

Because everything you calculated would actually happen continuously and instantly in the real world, there is no perfect order to put your calculations in. When the time step is smaller, your calculations are closer to the continuous situation, regardless of order, and the answers should get more accurate. Your original time step of dt=0.25 at an initial velocity of 35 m/s allowed a lot of motion (almost 10 meters) between calculations. That is too much motion for the accuracy you want. A calculation rate of 400 per second is not unreasonable. There are situations (like a car on the ground where the suspension spring compression depends on inches above the ground) where calculation rates of thousands per second are required. Advanced simulation tools can monitor how rapidly things are changing in the simulation of continuous processes and adjust the time step size appropriately as it progresses through simulated time.

ok so this is were I am now

the graph needs to look like:

but I can't get it right. I have used smaller and smaller timeSteps but my tailwind is pushing the ball too high.

based on this in the textbook:

I wrote this:

%x() and y() are the positions of the projectile
%dt = time step
%v_init = initial speed
%theta = launch angle
%B_m = proportional to drag force = B2/m
close all
clear all
clc

%define Variables and Matrices
timeStep = .000001;
initialPositionX = 0;
initialPositionY = 1;
initialVelocity = 110*0.44704; %mph to m/s
positionXNoWind = zeros(1,50);
positionYNoWind = zeros(1,50);
positionXNoWind(1) = initialPositionX;
positionYNoWind(1) = initialPositionY;
theta = 35 * 0.0174533; %degrees to radians
initialVelocityX = initialVelocity * cos(theta);
initialVelocityY = initialVelocity * sin(theta);
vd = 35; %m/s
delta = 5; %m/s
gravity = -9.8;
maxCalculations=100000000;

Bm = .0039 + (.0058)/(1+exp((initialVelocity-vd)/delta)); %B2/m

velocity = initialVelocity;
velocityX = initialVelocityX;
velocityY = initialVelocityY;

velocityWind = 0 * 0.44704; %mph to m/s

for i = 2:maxCalculations
    positionXNoWind(i) = positionXNoWind(i-1) + velocityX * timeStep;
    positionYNoWind(i) = positionYNoWind(i-1) + velocityY * timeStep;
    velocity = sqrt(velocityX^2 + velocityY^2);
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));
    dragForce = Bm * (velocity - velocityWind);
    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep);
    velocityX = velocityX - (dragForce * (velocityX - velocityWind) * timeStep);
    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep
    %velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    %velocityX = velocityX - (dragForce * velocityX * timeStep)
    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)
    %positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep
    %positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep
    %Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    if positionYNoWind(i) <= 0
        break
    end
end

positionXTailWind = zeros(1,50);
positionYTailWind = zeros(1,50);
positionXTailWind(1) = initialPositionX;
positionYTailWind(1) = initialPositionY;

velocity = initialVelocity;
velocityX = initialVelocityX;
velocityY = initialVelocityY;
velocityWind = 10 * 0.44704; %mph to m/s

for i = 2:maxCalculations
    positionXTailWind(i) = positionXTailWind(i-1) + velocityX * timeStep;
    positionYTailWind(i) = positionYTailWind(i-1) + velocityY * timeStep;
    velocity = sqrt(velocityX^2 + velocityY^2);
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));
    dragForce = Bm * (velocity - velocityWind);
    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep);
    velocityX = velocityX - (dragForce * (velocityX - velocityWind) * timeStep);
    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep
    %velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    %velocityX = velocityX - (dragForce * velocityX * timeStep)
    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)
    %positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep
    %positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep
    %Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    if positionYTailWind(i) <= 0
        break
    end
endpositionXHeadWind = zeros(1,50);
positionYHeadWind = zeros(1,50);
positionXHeadWind(1) = initialPositionX;
positionYHeadWind(1) = initialPositionY;

velocity = initialVelocity;
velocityX = initialVelocityX;
velocityY = initialVelocityY;
velocityWind = -10 * 0.44704; %mph to m/sfor i = 2:maxCalculations
    positionXHeadWind(i) = positionXHeadWind(i-1) + velocityX * timeStep;
    positionYHeadWind(i) = positionYHeadWind(i-1) + velocityY * timeStep;
    velocity = sqrt(velocityX^2 + velocityY^2);
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));
    dragForce = Bm * (velocity - velocityWind);
    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep);
    velocityX = velocityX - (dragForce * (velocityX - velocityWind) * timeStep);
    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep
    %velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    %velocityX = velocityX - (dragForce * velocityX * timeStep)
    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)
    %positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep
    %positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep
    %Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    if positionYHeadWind(i) <= 0
        break
    end
end
%a = -positionY(i) / positionY(i-1)
%positionX(i) = (positionX(i) + (a * positionX(i-1))) / (1 + a)
%positionY(i) = 0

%%Plots
figure(1)
hold on
box on
plot(positionXNoWind,positionYNoWind,'-k',positionXTailWind,positionYTailWind,':k',positionXHeadWind,positionYHeadWind,'-.k')
set(gca,'Xtick',linspace(0,150,4),'fontsize',18,'Ytick',linspace(0,50,6))
set(gcf,'Color','w');
set(gcf,'Resize','on');

ylim([0 30])
xlim([0 150])
hold off

The old formula was B_2*v*v_x
so I interpreted that formula as being B_2*(v-v_wind)*(V_x-v_wind) when I rewrote the formulas in my for loop.
unfortunately it didn't work. so I did something wrong. I get:

I also tried splitting my formula into an x and y component when I did the subtraction. wind is completely in the x direction. no y component.
so instead of B*(v-wind) * ... I did (sqrt((v_x-v_wind)^2+(v_y)^2) and likewise.
I got:

%x() and y() are the positions of the projectile
%dt = time step
%v_init = initial speed
%theta = launch angle
%B_m = proportional to drag force = B2/m
close all
clear all
clc

%define Variables and Matrices
timeStep = .000001;
initialPositionX = 0;
initialPositionY = 1;
initialVelocity = 110*0.44704; %mph to m/s
positionXNoWind = zeros(1,50);
positionYNoWind = zeros(1,50);
positionXNoWind(1) = initialPositionX;
positionYNoWind(1) = initialPositionY;
theta = 35 * 0.0174533; %degrees to radians
initialVelocityX = initialVelocity * cos(theta);
initialVelocityY = initialVelocity * sin(theta);
vd = 35; %m/s
delta = 5; %m/s
gravity = -9.8;
maxCalculations=100000000;

Bm = .0039 + (.0058)/(1+exp((initialVelocity-vd)/delta)); %B2/m

velocity = initialVelocity;
velocityX = initialVelocityX;
velocityY = initialVelocityY;

velocityWind = 0 * 0.44704; %mph to m/s

for i = 2:maxCalculations
    positionXNoWind(i) = positionXNoWind(i-1) + velocityX * timeStep;
    positionYNoWind(i) = positionYNoWind(i-1) + velocityY * timeStep; 
    velocity = sqrt(velocityX^2 + velocityY^2);
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));
    dragForce = Bm * (sqrt((velocityX - velocityWind)^2 + velocityY^2));

    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep);
    velocityX = velocityX - (dragForce * (velocityX - velocityWind) * timeStep);
    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep 
    %velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    %velocityX = velocityX - (dragForce * velocityX * timeStep)
    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)
    %positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep
    %positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep
    %Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    if positionYNoWind(i) <= 0 
        break
    end
end

positionXTailWind = zeros(1,50);
positionYTailWind = zeros(1,50);
positionXTailWind(1) = initialPositionX;
positionYTailWind(1) = initialPositionY;

velocity = initialVelocity;
velocityX = initialVelocityX;
velocityY = initialVelocityY;
velocityWind = 10 * 0.44704; %mph to m/s

for i = 2:maxCalculations
    positionXTailWind(i) = positionXTailWind(i-1) + velocityX * timeStep;
    positionYTailWind(i) = positionYTailWind(i-1) + velocityY * timeStep; 
    velocity = sqrt(velocityX^2 + velocityY^2);
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));
    dragForce = Bm * (sqrt((velocityX - velocityWind)^2 + velocityY^2));
    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep);
    velocityX = velocityX - (dragForce * (velocityX - velocityWind) * timeStep);
    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep 
    %velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    %velocityX = velocityX - (dragForce * velocityX * timeStep)
    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)
    %positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep
    %positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep
    %Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    if positionYTailWind(i) <= 0 
        break
    end
endpositionXHeadWind = zeros(1,50);
positionYHeadWind = zeros(1,50);
positionXHeadWind(1) = initialPositionX;
positionYHeadWind(1) = initialPositionY;

velocity = initialVelocity;
velocityX = initialVelocityX;
velocityY = initialVelocityY;
velocityWind = -10 * 0.44704; %mph to m/sfor i = 2:maxCalculations
    positionXHeadWind(i) = positionXHeadWind(i-1) + velocityX * timeStep;
    positionYHeadWind(i) = positionYHeadWind(i-1) + velocityY * timeStep; 
    velocity = sqrt(velocityX^2 + velocityY^2);
    Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta));
    dragForce = Bm * (sqrt((velocityX - velocityWind)^2 + velocityY^2));
    velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep);
    velocityX = velocityX - (dragForce * (velocityX - velocityWind) * timeStep);
    %positionX(i) = positionX(i-1) + velocityX * timeStep
    %positionY(i) = positionY(i-1) + velocityY * timeStep 
    %velocityY = velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)
    %velocityX = velocityX - (dragForce * velocityX * timeStep)
    %initialVelocity = sqrt(initialVelocityX^2 + initialVelocityY^2)
    %positionX(i) = positionX(i-1) + (velocityX - (dragForce * velocityX * timeStep)) * timeStep
    %positionY(i) = positionY(i-1) + (velocityY - (9.8 * timeStep) - (dragForce * velocityY * timeStep)) * timeStep
    %Bm = .0039 + (.0058)/(1+exp((velocity-vd)/delta))
    if positionYHeadWind(i) <= 0 
        break
    end
end
%a = -positionY(i) / positionY(i-1)
%positionX(i) = (positionX(i) + (a * positionX(i-1))) / (1 + a)
%positionY(i) = 0

%%Plots
figure(1)
hold on
box on
plot(positionXNoWind,positionYNoWind,'-k',positionXTailWind,positionYTailWind,':k',positionXHeadWind,positionYHeadWind,'-.k')
set(gca,'Xtick',linspace(0,150,4),'fontsize',18,'Ytick',linspace(0,50,6))
set(gcf,'Color','w');
set(gcf,'Resize','on');

ylim([0 30])
xlim([0 150])
hold off

which looks pretty much the same

 

[grandpa2390]

made a more detailed graph to compare:

after trying to split components:

 

[haruspex]

my tailwind is pushing the ball too high.

So let's stop and think whether a tailwind should affect the height of the peak.
$F=k(v_x^2+v_y^2)$
$F_y=kv_y\sqrt{v_x^2+v_y^2}$
$\frac{\partial F_y}{\partial v_x}=k\frac{v_xv_y}{\sqrt{v_x^2+v_y^2}}$
The effect of a tailwind is to reduce the horizontal component of velocity when computing the drag. As you can see from the above, that reduces the vertical component of drag, so increases the maximum height.

 

[grandpa2390]

So let's stop and think whether a tailwind should affect the height of the peak.
$F=k(v_x^2+v_y^2)$
$F_y=kv_y\sqrt{v_x^2+v_y^2}$
$\frac{\partial F_y}{\partial v_x}=k\frac{v_xv_y}{\sqrt{v_x^2+v_y^2}}$
The effect of a tailwind is to reduce the horizontal component of velocity when computing the drag. As you can see from the above, that reduces the vertical component of drag, so increases the maximum height.

but it isn't supposed to. According to the textbook, it should give the ball a bit of extra force in the x direction and no effect in the Y component.

I created two separate Drag Forces. One for X and one for Y and got this

Maybe the code given by the author was just generalized? I feel like the landing points are slightly off. hopefully not too far off though.

 

[haruspex]

but it isn't supposed to. According to the textbook, it should give the ball a bit of extra force in the x direction and no effect in the Y component.

It depends whether the drag is taken to be linear or quadratic. From the code you copied, it is being taken as quadratic. That means a tailwind will reduce vertical component of drag and lead to a higher peak.
If the drag is linear the algebra is simpler. Horizontal and vertical drag become independent:
$F=k\sqrt{v_x^2+v_y^2}$
$F_y=kv_y$

 

[grandpa2390]

It depends whether the drag is taken to be linear or quadratic. From the code you copied, it is being taken as quadratic. That means a tailwind will reduce vertical component of drag and lead to a higher peak.
If the drag is linear the algebra is simpler. Horizontal and vertical drag become independent:
$F=k\sqrt{v_x^2+v_y^2}$
$F_y=kv_y$

I don't know what you mean by linear or quadratic. I do know that the force of the wind has only an x component

my baseball with no wind seems to land in the right spot. but the baseballs with wind seem to fall a bit shorter and bit further than the one in the textbook. Do you think I made a mistake?

 

[haruspex]

I don't know what you mean by linear or quadratic. I do know that the force of the wind has only an x component

Linear means the drag is proportional to the relative velocity. In vectors, if the wind has velocity $\vec w$ and the ball has velocity $\vec v$ then the relative velocity is $\vec v-\vec w$ and the drag force is $\vec F=-k(\vec v-\vec w)$ for some drag coefficient k.
As I wrote, linear drag is easy because you can treat the horizontal and vertical motions separately, so tailwinds and headwinds do not affect vertical velocity or height. Even though a headwind increases the overall drag force it does not affect the vertical component of the force.

Linear drag applies at low speeds. At higher speeds drag becomes quadratic, i.e. it rises as the square of the magnitude of the relative velocity: $\vec F=-k(\vec v-\vec w)|\vec v-\vec w|$.
I am pretty sure this would apply to a well-struck baseball.
The wind only has a horizontal velocity component, but the drag force is always along the line of relative velocity. With quadratic drag, that means an increase in relative horizontal velocity (such as with a headwind) increases not only the overall drag force but even the vertical component of it.

 

[FactChecker]

but it isn't supposed to. According to the textbook, it should give the ball a bit of extra force in the x direction and no effect in the Y component.

I created two separate Drag Forces. One for X and one for Y and got this
View attachment 221704

Maybe the code given by the author was just generalized? I feel like the landing points are slightly off. hopefully not too far off though.

This is a more realistic result of a horizontal wind than the one where the height was affected.

 

[haruspex]

This is a more realistic result of a horizontal wind than the one where the height was affected.

Why?

 

[FactChecker]

Why?

Often the drag and all aerodynamic forces are calculated in the wind axis and I don't think that a horizontal wind would have an effect on the height. The angle and magnitude of the initial velocity would change because the velocities would be wrt the wind.

PS. You may be correct in saying that their drag formula should cause the height to change. I haven't tried to figure that out. But I am not sure that we have the full definition of the variables and use of that formula. I am not an aerodynamics expert and the formula is nothing like what I have seen in actual use. (The things that I have seen used by aerodynamics people are not at all appropriate for a book example.)

 

[haruspex]

the drag and all aerodynamic forces are calculated in the wind axis

If by wind axis you mean the relative motion direction, yes, but here that is not horizontal.
Ever cycled in a crosswind? It'll slow you down whichever direction you go along the road.

 

[FactChecker]

If by wind axis you mean the relative motion direction, yes, but here that is not horizontal.

I meant that the wind is horizontal, not the relative motion.

Ever cycled in a crosswind? It'll slow you down whichever direction you go along the road.

That is because you are expending force and energy to keep going straight on the road, so in effect you are steering into the wind. A thrown ball just goes with a cross wind. The same is true of an airplane that is not "crabbed" into the wind. There would be an initial velocity pointed into the wind but there would be no opposition to the wind.

 

[grandpa2390]

I meant that the wind is horizontal, not the relative motion.That is because you are expending force and energy to keep going straight on the road, so in effect you are steering into the wind. A thrown ball just goes with a cross wind. The same is true of an airplane that is not "crabbed" into the wind. There would be an initial velocity pointed into the wind but there would be no opposition to the wind.

I agree with you. Not jut because the graph in the book says that the height is not affected. but this wind is very specifically in one dimension.

Just like the force of gravity doesn't affect the distance the ball travels, just the height it reaches.

 

[grandpa2390]

Linear means the drag is proportional to the relative velocity. In vectors, if the wind has velocity $\vec w$ and the ball has velocity $\vec v$ then the relative velocity is $\vec v-\vec w$ and the drag force is $\vec F=-k(\vec v-\vec w)$ for some drag coefficient k.
As I wrote, linear drag is easy because you can treat the horizontal and vertical motions separately, so tailwinds and headwinds do not affect vertical velocity or height. Even though a headwind increases the overall drag force it does not affect the vertical component of the force.

Linear drag applies at low speeds. At higher speeds drag becomes quadratic, i.e. it rises as the square of the magnitude of the relative velocity: $\vec F=-k(\vec v-\vec w)|\vec v-\vec w|$.
I am pretty sure this would apply to a well-struck baseball.
The wind only has a horizontal velocity component, but the drag force is always along the line of relative velocity. With quadratic drag, that means an increase in relative horizontal velocity (such as with a headwind) increases not only the overall drag force but even the vertical component of it.

the drag coefficient does get smaller as the ball moves faster, but I believe that's already been factored into the equation given by the author for Bm

I don't know. it makes the graph look more correct (according to the book), but as much as I want to say the equation is generalized, the author wrote the equations specifically for when the drag is only pointed toward or against the ball. so they are specific... but they don't work.

 

[FactChecker]

I don't know. it makes the graph look more correct (according to the book), but as much as I want to say the equation is generalized, the author wrote the equations specifically for when the drag is only pointed toward or against the ball. so they are specific... but they don't work.

A good place to look for some information about drag on a sphere is on the NASA website https://www.grc.nasa.gov/www/k-12/airplane/dragsphere.html. NASA does so much work in this area that they are a "must-know" resource. Other NASA drag coefficient information is at https://www.grc.nasa.gov/www/k-12/airplane/dragco.html .

 

[grandpa2390]

A good place to look for some information about drag on a sphere is on the NASA website https://www.grc.nasa.gov/www/k-12/airplane/dragsphere.html. NASA does so much work in this area that they are a "must-know" resource. Other NASA drag coefficient information is at https://www.grc.nasa.gov/www/k-12/airplane/dragco.html .

but a baseball isn't a sphere. it has a rough surface that gives it a better drag over a sphere :)

 

[FactChecker]

but a baseball isn't a sphere. it has a rough surface that gives it a better drag over a sphere :)

They have a page just for baseballs. https://www.grc.nasa.gov/www/k-12/baseball/index.html

 

[haruspex]

I meant that the wind is horizontal, not the relative motion.

Yes, I thought that was what you meant, so I disagree with your statement.

That is because you are expending force and energy to keep going straight on the road, so in effect you are steering into the wind. A thrown ball just goes with a cross wind. The same is true of an airplane that is not "crabbed" into the wind

In those cases you cite, the projectile has, more or less, acquired the same lateral velocity as the wind, so there effectively is no wind.
For the bicycle, one's intuition may be that the lateral static friction from the wheels will counter the crosswind. Indeed, at low speed, with a linear drag, this is correct; the crosswind should not slow you at all. It is the quadratic drag which makes crosswinds a problem for cyclists.

Have you looked through equations I posted? Can you find a flaw there?

 

[FactChecker]

For the bicycle, one's intuition may be that the lateral static friction from the wheels will counter the crosswind.

In a crosswind, the bike will lean into the wind in a way that would otherwise cause it to turn in the direction of the wind. That turn is opposed by the wind and there is an associated increase in work required to maintain a steady speed in a straight line.

Indeed, at low speed, with a linear drag, this is correct; the crosswind should not slow you at all. It is the quadratic drag which makes crosswinds a problem for cyclists.

I have always considered drag to be proportional to the velocity squared, not linear.

Have you looked through equations I posted? Can you find a flaw there?

I see your point. I can't see an error.

 

[haruspex]

the bike will lean into the wind

Yes.

That turn

What turn? The bike still goes in a straight line, and the front wheel still points straight ahead.
The lateral static friction at the road contact counters the lateral component of the drag, while the net torque from those two is balanced by the torque from the gravitation/normal force pair.

I downloaded the NASA baseball applet, but I can't get it to work. It puts up a page with a banner naming the applet etc., but the rest of the page is blank. Tried it with both Google Chrome and IE.