- #1
Apollinaria
- 82
- 0
Another one.. I'm sorry but I will likely spend tomorrow and today here with you guys asking for help and mooching solutions. Same deal, badly explained unit. We spent 15 minutes on this. Attached questions as jpg...
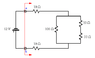
How do I find total equivalent resistance? What does that even mean? And power dissipated? What? :grumpy:
No idea...
I understand sometimes you add resistances and sometimes you add inverse resistances?
Can somebody please dumb this down into simple terms and try to explain step by step? Obviously I'm willing to work this through on paper with some help, guidance and feedback. I really want to understand the concept behind this.
Homework Statement
How do I find total equivalent resistance? What does that even mean? And power dissipated? What? :grumpy:
Homework Equations
No idea...
The Attempt at a Solution
I understand sometimes you add resistances and sometimes you add inverse resistances?
Can somebody please dumb this down into simple terms and try to explain step by step? Obviously I'm willing to work this through on paper with some help, guidance and feedback. I really want to understand the concept behind this.


 +
+  +
+