What Magnetic Forces Act Between Parallel Current-Carrying Wires?

[barnsworth]

1) Four long, straight, parallel wires each carry current I. In plane perpendicular to the wires, the wires are at the corners of a square of side "a". Find the force per unit length on one of the wires if (a) all the currents are in the same direction, and (b) all the currents are in the opposite direction.

I got “0” for both parts (a) and (b) because when I use the right-hand rule, all B’s seem to cancel out, so F / l would invariably be 0, but this seems overly simple.

here's #2...

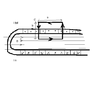
2) A solenoid carries “n” turns per unit length. Apply Ampere’s law to the rectangular curve shown to derive an expression for B assuming that it is uniform inside the solenoid and zero outside it.

I have no idea how to do this. I know that Ampere's Law is \oint B*dl = \mu*I, and the answer should be B = \frac{1}{2}\mu n I ( \frac{b}{\sqrt{b^2 + R^2}} + \frac{a}{\sqrt{a^2 + R^2}}). I don't even understand the diagram. Can somebody get me started on this?

thx for any help in advance.

 

[whozum]

For #1:
The direction of B depends on the direction of I, so if they canceled out for parallel then they can not cancel out for antiparallel. I'm not sure of the solution to this one but I know that fact. I'm thinking F = ILB but I am probably wrong.

For #2:
Its a closed integral, and you will be integrating along the perimeter of the rectangle with lengths a and b. if B is uniform then it is constant, and your integral simplifies to B*int{dl} . Now you have to relate the infinitesimal length 'l' to the radius of the loop R, and solve for B.

Notice in the solution you provided that the integral involves partial fraction decomposition. You can work backwards from this integral to reconstruct the integrand, and perhaps with this information the problem would be easier for you to understand.

 

[thepatientmental]

Hello,

For the first question, you are correct in your reasoning. The force per unit length on one wire due to the other three wires will be zero because the magnetic fields created by each wire will cancel out due to their parallel arrangement. This is a common occurrence in physics, where the net effect of multiple forces or fields can be zero.

For the second question, let's break it down step by step. First, we need to understand the diagram. It shows a rectangular curve, which represents the path of integration for Ampere's Law. The solenoid is shown as a long, cylindrical object with "n" turns per unit length. This means that as you move along the length of the solenoid, you will encounter "n" loops of wire per unit length.

Now, we can apply Ampere's Law to this situation. As you mentioned, Ampere's Law states that the integral of the magnetic field around a closed loop is equal to the product of the permeability of free space (μ) and the current enclosed by the loop. In this case, the current enclosed is simply the current passing through each loop of the solenoid, which is equal to nI (since there are "n" loops per unit length and each loop carries a current of I).

Next, we need to determine the path of integration for the integral in Ampere's Law. In this case, it is the rectangular curve shown in the diagram. We can write the integral as:

∫B*dl = μ*nI

Now, we need to determine the value of B. Since we are assuming that the magnetic field is uniform inside the solenoid and zero outside, we can use the formula for the magnetic field inside a solenoid, which is:

B = μ*nI

Plugging this into the integral, we get:

∫(μ*nI)*dl = μ*nI

Next, we need to evaluate the integral. Since the path of integration is a rectangle, we can break it down into four segments: the top, bottom, left, and right sides. Each of these segments will have a length and a direction of integration (clockwise or counterclockwise). For simplicity, let's assume that the integration is clockwise for all four segments. This means that the top and bottom segments will have a length of "b" and the left and right segments will have a length of "a".

Plugging in these