- #1
Maxo
- 160
- 1
When looking at the shape of an airplane wing from the side, like here
 I'm wondering what makes the air move faster above the wing. I have some questions about this:
I'm wondering what makes the air move faster above the wing. I have some questions about this:
1. It rather looks like there is a longer distance for the air to travel above the wing than below it, but wouldn't a longer travel distance rather imply less speed? Why doesn't it?
2. It also looks like the air must "bend" more when going on top of the wing than below it (more easily seen here:
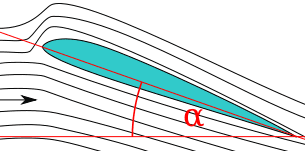 ), wouldn't that also create more air resistance on top of the wing and thereby less speed? Why doesn't it?
), wouldn't that also create more air resistance on top of the wing and thereby less speed? Why doesn't it?
3. What is it that makes the air move faster above the wing?
1. It rather looks like there is a longer distance for the air to travel above the wing than below it, but wouldn't a longer travel distance rather imply less speed? Why doesn't it?
2. It also looks like the air must "bend" more when going on top of the wing than below it (more easily seen here:
3. What is it that makes the air move faster above the wing?
Last edited by a moderator: