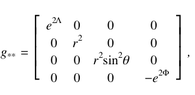Pyter said:
how would you find the latitude and longitude of two points on the Earth's surface without leaving it, using only curved rulers or light/radio waves running along its surface?
You wouldn't. Latitude and longitude are global coordinates, not local ones. You can't find them by purely local measurements.
If you wanted to find the metric of the Earth's surface based on purely local measurements within the surface, here is how you would proceed, by analogy with how the corresponding task would be done in GR:
(1) Set up local coordinates any way you want. The usual method would be to start by labeling the point where you are as ##(0, 0)##, and then marking out two perpendicular straight lines through that point and labeling them as your two different coordinate axes. Strictly speaking, there is no requirement for the coordinate axes to be perpendicular, only linearly independent; but making them perpendicular, at least locally, makes the calculations easier when you want to compute the curvature.
(2) Pick one coordinate axis, call it ##a## (I'll avoid using the standard Cartesian names since we will be finding that the manifold in question is not flat), and mark off equal increments of some convenient unit distance (such as the length of your meter stick) along it from ##(0, 0)##. Then mark out perpendicular straight lines crossing the axis at each of your marked points. At each of the crossing points, these perpendicular straight lines will be tangent to the coordinate grid lines for your other coordinate, call it ##b##.
(3) Extend each of the perpendicular straight lines by purely local means--i.e., just looking at that particular line and keeping it straight by extending it in the same direction the way a surveyor would, without regard to its relationship with any neighboring lines--and see if they converge or diverge. If they do, the manifold is curved, at least in that local region. If they don't, the manifold is flat, at least in that local region.
On Earth, you will find that the lines converge (globally, what you are doing is drawing segments of adjacent great circles that all start off crossing another great circle at right angles, and those will of course converge), indicating that the manifold is curved. By measuring the rate of convergence, you can find the numerical value of the curvature (which, since this is a 2-dimensional manifold, will just be a single number; to put it another way, the Riemann tensor of this manifold has only one component).
In terms of your local coordinate chart, you will find that the perpendicular straight lines you have drawn will not be identical with the coordinate grid lines of ##b##. In terms of the metric written in this coordinate chart, you will find that it looks exactly Euclidean at point ##(0, 0)##, but picks up non-Euclidean terms as you move away from ##(0, 0)##. (Obviously, then, these coordinates are
not latitude and longitude, as I said above.)
The method I have described above is analogous to setting up what are called Riemann normal coordinates in GR, centered on a chosen point of spacetime. These coordinates are chosen to "look Minkowskian" at the chosen point, just as the coordinates I described above "look Euclidean" at the chosen point. Most GR textbooks discuss this at a fairly early point in their exposition.