Wheatstone bridge and conditions for current to flow between 2 points

[fog37]

Hello,

I was reflecting on the functioning of a balanced Wheatstone bridge circuit:

Point C and D are at the same electric potential V (zero potential difference). Even if they are connected by an ideal zero resistance wire, current will not split at either node C or D to flow through that section between C and D.

So what are the conditions for a current to flow along a path between two points in a circuit?

In the a basic DC circuit below composed of a battery with $\Delta V=12 V$, perfectly conducting wires (zero resistance), and single resistor with $R=2 \Omega$, a nonzero electrical current $I =6A$ flows between points a and b ($V_a- V_b \ne 0$ and nonzero resistance) and between points c and d ($V_a- V_b = 0$ and zero resistance between them).

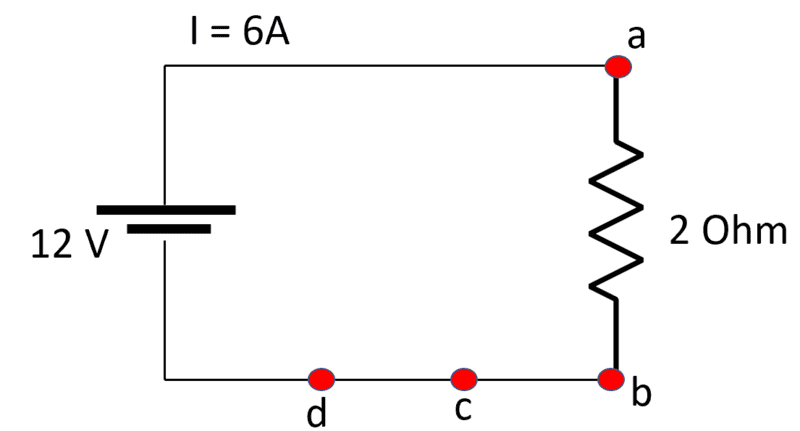
I would say that nonzero current ALWAYS flows if there is nonzero potential difference AND a finite resistance between two points (ex: current flowing from a to b).
A nonzero current CAN also flow there is zero potential difference between the points but the resistance must be zero between them (ex: current I flowing from c to d). But that is not always the case as it happens in balanced Wheatstone bridge between point C and D...

Is my thinking that correct? More fundamentally, a current will flow if there is a nonzero E field inside the path between the points to push and move the electric charges.

Thanks!

 

[andrewkirk]

I would agree with your thinking but find it unnecessary, because we never have a zero resistance wire. There is always some resistance. It just might be really small. If there's a really small resistance, we will also have a really small potential difference, so everything works out fine.

This example serves to illustrate a general principle in physical reasoning. We regularly make impossible assumptions, such as massless, non-stretchable strings, incompressible solids and perfectly rigid levers, in order to simplify calculations, and that's fine. But as soon as the impossible assumptions start to cause problems, dilemmas or ambiguities, we should drop them.

BTW, to work out the flow of current from C to D, calculate the flows through R1-R4 in a circuit the same as above but with the segment CD collapsed to a point. Then we can infer from Kirchhoff's circuit laws that in the original circuit, the current from C to D is R4 - R3 (which equals R1 - R2).

 

[DaveE]

I would say that nonzero current ALWAYS flows if there is nonzero potential difference AND a finite resistance between two points (ex: current flowing from a to b).

Yes.

A nonzero current CAN also flow there is zero potential difference between the points

No. With no potential difference there is nothing, on average, to move the electrons. They will stay bound to atoms, or bounce around at random with thermal energy. Free electrons repel each other so they like to spread out. If they are going towards the same place, something is pushing them that way.

 

[Baluncore]

I would say that nonzero current ALWAYS flows if there is nonzero potential difference AND a finite resistance between two points (ex: current flowing from a to b).

That is a simple statement of Ohm's Law.

 

[hutchphd]

I do not understand the question. In my experience the function of the bridge is to make a null voltage measurement. The path from C to D is a very high impedance voltage measuring device. The shorted version (wire from C to D is not a Wheatstone bridge: It is a two (parallel composite) resistors in series.

.

 

[DaveE]

It's not really a question about the bridge circuit is it? That's just the first paragraph which isn't really referenced in the following questions about what makes electrons in conductors move.

 

[DaveE]

And now, for something completely different. TIL Wheatstone was a jerk.

 

[hutchphd]

It's not really a question about the bridge circuit is it?

Yes sorry I missed that.
I still dislike the invocation of ohm's law to justify the zero current. It follows simply from charge conservation (or Kirchhoff's current Law if you prefer) without mention of Ohm. But now I am arguing Dogma so I will cease!

 

[sophiecentaur]

So what are the conditions for a current to flow along a path between two points in a circuit?

It worries me that I go no return for a search for "ratio" in this thread which is about the Wheatstone Bridge. The current between C and D will only be zero when the ratios of the resistors on either side are equal. In that case, the circuit can be treated as a very much simpler layout. Once the ratios are not equal, the actual value of resistance between C and D will talk and the whole circuit needs to be analysed in full.