Potential difference on circuit conductors....

[fog37]

Hello Forum,

Consider a simple DC circuit composed of a battery (say 2V), conducting wires and a single resistor R=2 Ohm

The potential difference across the resistor will be exactly 2V only if the wires were superconductors (zero resistance). But wires do have some small finite resistance so, in practice, there is a tiny potential difference between any two points on each conducting wire, correct? The presence of a nonzero (even if small) potential difference implies the presence of an electric field E=Delta_V/d between points separated by distance d.

This nonzero electric field E exists and is longitudinal both on the surface of the wire and inside the wire, correct?

If the wires were superconducting (truly zero resistance), a DC current would still flow in them. The current is determined and limited by the 2Ohm resistor. The wires now have a nonzero current but zero resistance. From Ohm's law J=sigma*E, the electric field is zero in this case which means that there is no effort (and no energy loss) in moving the charges inside the wires to produce the current. The wires would be equipotential conductor (situation different from the equipotential conductors in electrostatics where there is no net moving charge inside the conductor volumes and the E field is normal to the surface)

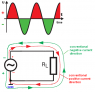
Does the same happen in AC circuits, i.e. there is a small but nonzero potential difference between any pairs of points on the same conductor, if the voltage source was time-varying? Clearly, there is a potential difference between the different conducting wires since they are connected to the two different terminals of the voltage source...

Thanks,
fog37

 

[Jony130]

But AC voltage is nothing more than a a constantly changing DC voltage. So why should AC voltage behave differently?

 

[fog37]

jony130,

thank you. That is a fair comment.

I guess in the AC case the current is alternating and is positive and negative (different directions) and zero on different points of the same conducting wire. That induced me to think that these different current values along the wire corresponded to different charge densities on or within the wire and charge densities of different sign but separated from each other would create an electric field, hence a potential difference...but apparently that is not the case...

I recently read an article that explains how "surface" charges exist on the surface of wires in a DC circuit:
[/PLAIN] http://science.uniserve.edu.au/school/curric/stage6/phys/stw2002/sefton.pdf[/URL]

That made me thing about what happens in the case of an AC circuit. I guess the surface charges are positive and negative in different parts of the same wires...

In RF circuit, where voltage and currents are time-varying, one conductor (a ground plane, for example) is chosen as the reference conductor. Sometimes this conductor is grounded or floating (not connected to ground) and represent the return conductor (even if current does not really return since it is AC and simply oscillates back and forth)...
I guess it is assume that conductor is equipotential due to the fact that its resistance is so negligible...

thanks,
fog37

 

[Jony130]

We can always freeze the AC voltage and treat is as a "DC voltage" maybe not literally. Because for example we can have a battery a switch to change the battery polarity and a pot. So we can very the voltage and change the polarity with frequency 50Hz.
For example if we have a sine wave signal source with the amplitude 10Vpeak and frequency of 50Hz.
So for t = 0s -->Vs = 0V so no current is flowing.
At t = 1.7ms ---> Vs = 10V*sin(314*1.7m) = 10V*sin(0.534 rad) = 10V * 0.509 = 5.09Vpeak
at t = 5ms --->Vs = 10V*sin(314*5ms) = 10Vpeak
at t = 10ms -->Vs = 10V*sin(314*10ms) = 0V
at t = 11.7ms--->Vs = 10V*sin(314*11.7m) = -5.07Vpeak
at t = 15ms --->Vs = 10V*sin(314*15ms) = - 10V

 

[sophiecentaur]

We can always freeze the AC voltage and treat is as a "DC voltage"

That only works when the frequency is low enough to allow you to ignore the reactive nature of any circuit. Once you have reactive elements, the relationship between instantaneous PD and Current is no longer proportional - because of the phase shifts involved. The internal fields in the circuit will be affected by these phase shifts. Many AC appliances have a Power Factor that is significantly different from unity.

 

[William White]

Does the same happen in AC circuits, i.e. there is a small but nonzero potential difference between any pairs of points on the same conductor,

The difference between two adjacent points is negligible; but at the opposite ends of a very long conductor, say a distribution cable, or even more so, a transmission line, the potential differences can be considerable and increase with the current. This is why power is distributed and transmitted high voltages (and relatively low current). If your potential difference (volt drop) between two points was, say 240V and you are distributing at 240V, you are in trouble, you've lost 100% of your power, dissipated by the resistance of the conductor. If you are distributing at 6350 V (11kv) you've lost just 4% of your power; at 230 kV (400KV) you've lost 0.1% of your power.

Its best to think of the conductor as a long resistor, and if there are loads connected in parallel, then as a lot of resistors in series.

Calculating volt drop is an important thing to do when designing your circuit - you need to ensure there are enough volts at the far end. If not, you need to use a bigger conductor.What you might find interesting, is that AC current tends to flow near the surface of a conductor. In a substation, this is used to advantage by making the over-head busbars hollow.
https://en.wikipedia.org/wiki/Skin_effect

 

[sophiecentaur]

If your potential difference (volt drop) between two points was, say 240V and you are distributing at 240V, you are in trouble, you've lost 100% of your power, dissipated by the resistance of the conductor.

A bit of an oversimplification there because you are assuming that the resistance of the Load is Zero. To work out exactly the effect (power loss) due to cable resistance, you really need to work out the current through the total circuit resistance and then do I²R_{supply cable} and the same for the Load Resistance.

 

[William White]

A bit of an oversimplification...

there is no need to over-complicate

the simplification is fine for its purpose

 

[sophiecentaur]

there is no need to over-complicate

the simplification is fine

I don't really agree. An example which actually makes sense would have been a good illustration of the effect and, at the same time, been correct. This particular oversimplification can lead people astray - and to no purpose. The fact is that series R in the supply also has the effect of reducing the volts across the load. If you want to reduce the received volts to Zero then the series resistance is so high as to result in almost zero power loss - just no power being delivered. The Maximum Power Theorem applies here, if we are being precise and it's where the load and source resistances are equal that the effect is worst. Not Rocket Science and easy to assimilate. We should assume that the questioner has the potential to take that sort of thing on board.

 

[fog37]

Thanks everyone.

In a DC circuit where a battery connected a load (resistor) via realistic wires, there is a potential difference between the two wires (each wire connected to a different terminal of the battery) and there is also a small potential difference between any pair of points on the same wires. The closer the points on the same wire the smaller the potential difference. Only if the wires were superconducting (truly zero resistance) the potential difference would be zero even if current is flowing through the wire itself since there is no electric field need to maintain the current in that section of the wire. So superconducting wires would be equipotential in the sense that each point on the wire has the same potential but two points (each one on a different wire) have a potential difference.

That said, I think the same concepts apply to AC circuits, i.e. if the wires had zero resistance there would be no potential difference between points on the same wires. In the AC case current (flow of charges) move back and forth and I think volume net charge densities (either positive or negative )develop at different points along and inside the wire. I would think that these charge density, being of different sign, would create an electric field between them. Since Delta_V= - E d, having an electric field would imply having a potential difference in the AC situation even if the wires were superconducting...

 

[sophiecentaur]

if the wires had zero resistance there would be no potential difference between points on the same wires.

Yes there would (a small one). This is because of the Inductance, which introduces a phase shift and a consequently finite difference in Potential. You need to consider both Magnetic and Electric fields when you launch into AC.

 

[fog37]

thank you sophiecentaur.

Good point. I guess when we deal with AC currents and their frequency (Hz) we need to take into account that:

a) the wire resistivity remains the same at every frequency (Hz) but the AC current starts flowing only towards the edges of the conducting wires. This is the skin effect and can be interpreted as the wire having a smaller "effective cross-section", hence a higher resistance (skin resistance). But maybe also the resistivity changes with frequency the same way index of refraction changes with frequency (dispersion)

b) there are reactive effects due to inductance and capacitance of the resistor itself. In fact, a real resistor is modeled with a parallel stray capacitance and a series inductance and resistance. Let's assume the resistance is zero. There is stray capacitance between the resistor two terminals because they behave like the plates of a capacitor. For that to happen the two terminals must have differently signed charge on them. The series inductance is due also to the presence of charge accumulations that create an electric field that opposes the flow on the main current. Capacitative and inductive impedances don't consume power (only absorb and give back) but still create a hindrance to the flow of charge. Whenever there is an electric field we can think that there is a potential difference. The "positive charges" in conventional current must climb that potential slope...

thanks!
fog37

 

[Jyothish]

In the case of AC , opposition to the current flow depends also on the frequency involved.Every conductor, whether super conductor or not, will have a non zero self inductance.This means the conductor is linked by its own flux.When a time varying current flows, the resultant time varying flux linkage will produce an electric field inside the conductor.This aids or oppose the current depending on whether current is decreasing or increasing.Skin effect is due this this property.However, in lower frequencies we ignore this effect in small circuits.However it matters and to be included in calculation in the case of long distance power transmission lines, or when the frequency is very high

 

[fog37]

Thanks Jyothish.

I did find and interesting article on this same topic: http://www.edn.com/design/components-and-packaging/4423492/Resistors-aren-t-resistors

And at page 20 of[/PLAIN] http://www.egr.msu.edu/em/research/goali/notes/module5_nonideal_behavior.pdf[/URL]

When the topic of two-wire transmission lines, I wonder why the only voltage that is considered is the voltage wave V(z), where V(z) is the potential difference between the two individual wires. As you mention, if the frequency is high enough, there is also a potential difference between points on the same wire due to the inductive and capacitative reactance... Why is that voltage not mentioned?

 

[Jyothish]

Thanks Jyothish.

I did find and interesting article on this same topic: http://www.edn.com/design/components-and-packaging/4423492/Resistors-aren-t-resistors

And at page 20 of[/PLAIN] http://www.egr.msu.edu/em/research/goali/notes/module5_nonideal_behavior.pdf[/URL]

When the topic of two-wire transmission lines, I wonder why the only voltage that is considered is the voltage wave V(z), where V(z) is the potential difference between the two individual wires. As you mention, if the frequency is high enough, there is also a potential difference between points on the same wire due to the inductive and capacitative reactance... Why is that voltage not mentioned?

Unable to open the second link.I guess, your question is related to this document

 

[Baluncore]

When the topic of two-wire transmission lines, I wonder why the only voltage that is considered is the voltage wave V(z), where V(z) is the potential difference between the two individual wires. As you mention, if the frequency is high enough, there is also a potential difference between points on the same wire due to the inductive and capacitative reactance... Why is that voltage not mentioned?

If the voltage on the wire is an AC signal, then at any instant there will be a voltage difference between different points on the same wire due to the propagation delay of the signal on the line. The speed of propagation is the velocity factor which is proportional to 1 / Sqrt( L*C ). The effects of L and C are implicitly recognised and so do not need to be mentioned.

 

[fog37]

Thanks Baluncore. I see that the EM wave propagates along the line at the speed you mentioned.

The distributed capacitance C refers to the capacitance between the two wires, correct? It is not referring to the self-capacitance of each wire.

As far as L, I guess it is the self-inductance of each wire.

 

[Baluncore]

The distributed capacitance C refers to the capacitance between the two wires, correct? It is not referring to the self-capacitance of each wire.

The capacitance is per short unit length of each wire to all it's environment, in all possible coupling modes.
Do you really believe that a single short element of a wire can have a self capacitance ?

As far as L, I guess it is the self-inductance of each wire.

The inductance per short unit length of each wire, but coupled to all other conductors and fields in it's environment.

For a regular geometry L & C would be replaced by the magnetic permeability, µ_r, and the electric permitivity, ε_r = dielectric constant.

At some point you must stop following the boundary between the infinite detail with complexity of the real world and the rational theory. The only thing you will find in that gap is a rise in confusion and an application for increasingly computationally intensive Finite Element Analysis.