When a black hole is formed officially?

[maxverywell]

When a black hole is formed officially from a collapsing star (consider the simplest case of spherically symmetric collapse of non-rotating spherical star)? I see two possible answers:

1) At the moment when the radius of the star crosses the event horizon ($r_{star}=r_s$) , but the singularity hasn't (?) been formed yet (it's inside the star, at its center, so it's not a singularity yet).

2) At the moment of creation of the singularity, i.e. when whole the star has collapsed to a point.

 

[Simon Bridge]

In anything to do with relativity, you should always place the observer - because the answers tend to depend on who is doing the looking.

Consider - for an observer stationary in the rest-frame of the collapsing star, a long way from it's center of mass, want's to use definition #2. How would they determine their own coordinate time for this situation?

 

[maxverywell]

An observer outside the event horizon at constant distance from it (stationary observer) won't see the star fully collapse, for him star's surface won't cross the event horizon. For an observer far away outside the event horizon it doesn't matter if the BH has been formed, because the spacetime is described by the Schwarzschild metric in any case.

An observer at the surface of the collapsing star is free falling. He will pass the event horizon and move towards r=0. He would use his proper time to measure when he will arrive at r=0.

But we can use Kruzkal coordinates V and U to describe the situation (no observer needed).
V is always timelike and U spacelike.
Is the BH formed when the surface of the star crosses the line V=U (the event horizon)?
Or is it formed when the surface of the star crosses the hyperbola $V=\sqrt{U^2+1}$?
Of course, the first case will become later the second, but formally when we consider that a BH is formed? I would say it's the second, because formally a BH is its singularity, event horizon and the spacetime inbetween. But for an outside observer it doesn't matter.

 

[Simon Bridge]

You have to define your terms - what do you mean when you say "a black hole has formed"?
Your question concerns definitions - so it is not physical. Make up any definitions you like.

 

[WannabeNewton]

Hi max! If we have a collapsing dust sphere and an observer sitting on the dust sphere, this observer will reach $r = 2M$ in finite proper time as read by a clock on the dust sphere. Let's say this observer sends out light signals to a distant observer who is stationary (i.e. following an orbit of the time-like killing vector field) at periodic intervals. The propagation time for the signals, for infinitesimal radial distances, is given by $dt = \frac{dr}{1 - r_g/r}$ hence the time interval to go from $r$ to the radial coordinate $r_0 > r, \forall r$ of the stationary observer will be given by $\Delta t = r_g \ln(\frac{\alpha}{r - r_g}) - r + \beta$. As you can see, $\lim_{r\rightarrow r_g} \Delta t = +\infty$ i.e. if the observer sends out a signal once he passes $r = 2M$ (which will be indicated by the proper time read on the clock riding on the dust sphere) the signal will never reach the external stationary observer; the observer will no longer be able to communicate with nor influence the external region. In other words, once the spherical collapse reaches past $r = 2M$, the black hole region is formed. See page 156 of Wald.

 

[maxverywell]

What about the observer sitting on the surface of the collapsing star? When is the BH formed for him?

 

[WannabeNewton]

He/she is riding on the collapsing sphere so whatever I said above applies to him/her.

 

[pervect]

Well, if we interpret the question "when is the black hole formed" as "when is the event horizion formed", the answer depends on exactly what you mean by "event horizon".

Various different definitions exist - you have the absolute horizon, the apparent horizon, and the Killing horizon. I have a feeling I'm missing a few other definitios of horizon, but I don't recall what they are.

The absolute horizon is only known in retrospect, since it requires an escape to infinity to define and such an escape takes infinite time. The Killing horizon requires symmetry to define - the symmetry in time in the exterior region can be represented by a "vector field" of vectors that are timelike in the exterior region. When these vectors become null vectors, you have the Killing horizon. The apparent horizon depends on the observer, very loosely speaking it has to do with whether bundles of light rays "spread out" or "contract". More exactly it has to to with the expansion scalar of null congruences.

I hope this quick overview helps, and that I haven't mangled anything too badly in the interst of intelligibility.

 

[WannabeNewton]

pervect I think max was implicitly talking about the absolute horizon (that's how I interpreted it anyways, hence why I talked about the formation from the point of view of the observer sitting on the collapsing sphere once he/she reaches past $r = 2M$). Geometrically, the killing horizon seems the most favorable. As background: in the Schwarzschild space-time the time-like killing field $\xi^{a}$ has a norm given by $\xi^{a}\xi_{a} = g_{\mu\nu}\xi^{\mu}\xi^{\nu} = -(1 - \frac{2GM}{r})$ so $\xi^{a}$ becomes null at $r = 2GM$. Since $\nabla^{a} r$ and $\xi^{a}$ become colinear at $r = 2GM$, $\xi^{a}$ will be normal to the surface defined by $r = 2GM$ (thus making it a null surface). Further, at $r = 2M$ $\xi^{a}$ will be tangent to the null geodesic generators of this killing horizon. For the Schwarzschild black hole, this killing horizon will coincide with its intrinsic event horizon (defined as $H = \text{cl}J^{-}(\mathcal{J^{+}}) \cap M$ where $M$ is the space-time).

However as pervect said, it should be noted that the notion of a killing horizon is independent from that of a black hole's event horizon in general.

 

[PeterDonis]

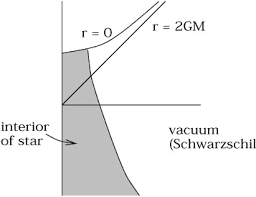
1) At the moment when the radius of the star crosses the event horizon ($r_{star}=r_s$) , but the singularity hasn't (?) been formed yet (it's inside the star, at its center, so it's not a singularity yet).

2) At the moment of creation of the singularity, i.e. when whole the star has collapsed to a point.

You actually missed one other possibility:

0) At the moment when the event horizon first forms. The EH forms at r = 0 and expands outward; it becomes fixed at r = 2M at the instant that the radius of the star crosses that radius.

Also, all of these definitions are observer-dependent, as others have already pointed out: "at the moment" implicitly requires a simultaneity convention, and there are different possible ones, some of which do not even cover the entire spacetime.

The "official" answer is that there is no official answer: there is no unique "moment when the black hole forms". There are the events we have listed, but none of them is officially "the" moment when the black hole forms.