When Is an Object Furthest from the Origin Given Its Position Vector?

[danpiz23]

Hi guys I posted a picture of the problem set and my work so far. I am on letter (d) of the problem set and I am stuck. I am 90% sure I have the formulas to solve (d) through (g) but I am not clear how. Can anyone give me a basic idea on what step I should take next?

Problem set

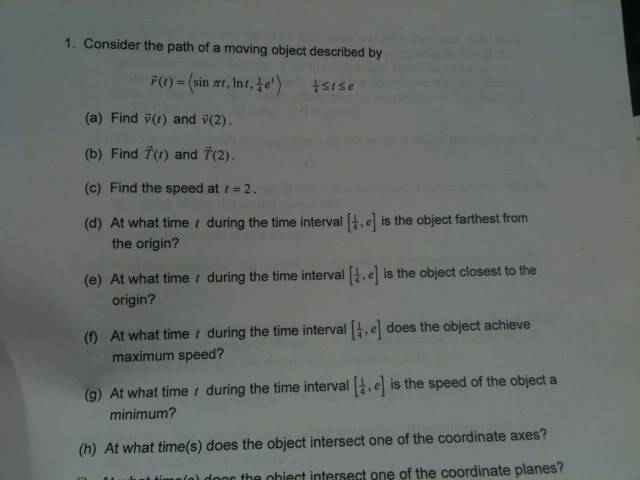
my work so far

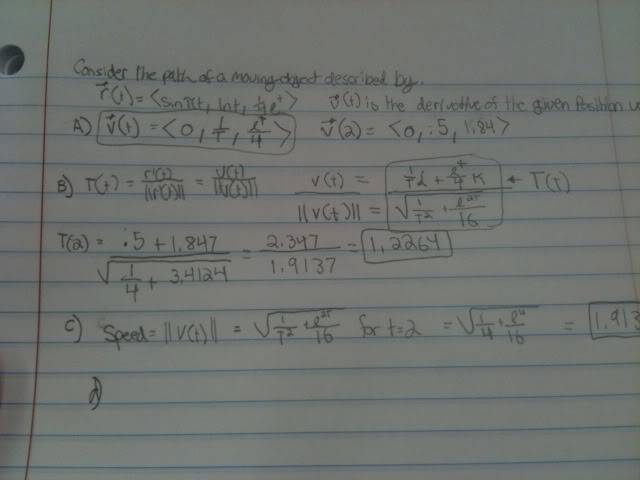
Thanks in advance for the help

 

[LCKurtz]

For (d) you just need to calculate when ||r(t)|| is min and max on the interval. It might be easier to work with ||r(t)||² and remember that the max and min of a function on a closed interval might occur at a critical point or an end point.

 

[danpiz23]

For (d) you just need to calculate when ||r(t)|| is min and max on the interval. It might be easier to work with ||r(t)||² and remember that the max and min of a function on a closed interval might occur at a critical point or an end point.

Thanks for the quick response. I understand the concept of finding the mix and max of the position vector within the given interval. Does this mean I can graph the position vector and just find the max and min between the given (t) interval?

Also I think I messed up on my work for part (b). Should the answer be written as a vector like this?

or a scalar quantity like I did in the first image I posted of the work I did??

 

[LCKurtz]

Your solution picture is difficult to read on my computer. All the answers for (a) and (b) are vectors, and the first component of v(t) and v(2) shouldn't be 0.

And presumably you aren't graphing the position vector. You are graphing its magnitude which is a scalar function of t.

 

[danpiz23]

I got zero for the first component because I took the derivative of the position vector r(t)

the derivative of the first component sin(pi)t = 0? not correct?
[PLAIN]http://www4c.wolframalpha.com/Calculate/MSP/MSP432419h9a63ehe63d19g00002afc315424ied1f7?MSPStoreType=image/gif&s=51&w=106&h=36

so answers for (a) and (b) should be in i,j,k vector format and Speed should be a single answer scalar format??

as far as finding the min and max, I think I understand the concept or what needs to be done. I just am not understand what to do with the position vector? Plug in the intervals given for t?

 

[LCKurtz]

I got zero for the first component because I took the derivative of the position vector r(t)

the derivative of the first component sin(pi)t = 0? not correct?
[PLAIN]http://www4c.wolframalpha.com/Calculate/MSP/MSP432419h9a63ehe63d19g00002afc315424ied1f7?MSPStoreType=image/gif&s=51&w=106&h=36

No. Wherever did you get that idea? The derivative of the sine function is the cosine function, and you need the chain rule.

so answers for (a) and (b) should be in i,j,k vector format and Speed should be a single answer scalar format??

Yes. Vectors are vectors and scalars are scalars.

as far as finding the min and max, I think I understand the concept or what needs to be done. I just am not understand what to do with the position vector? Plug in the intervals given for t?

You aren't maximizing or minimizing the position vector. You are working with its magnitude which is a scalar. Use normal calculus methods to find the max/min. See post #2.

 

[danpiz23]

Wow, Cannot believe I made such a big mistake finding the derivative of sin(pi)t. I typed it into wolfram alpha and just used that answer no questions.

This is the answer I came up with doing it with the chain rule...
derivative[sin(pi*x)] = cos(pi*T) * derivative[pi*T] = pi*cos(pi*T)

I understand that I need to use the magnitude of the position vector (||r(t)||), not quite sure how to find the max/min. I am looking up examples

 

[danpiz23]

I am still stumped on part (d), I am using Derive 6 to derive,simplify the problems. This is the work I have so far. Double checked all my work and looked online for examples, but I am not finding anything??

Is there a simple formula?? Do I just need to use limits or integration ??

 

[LCKurtz]

For (d) you just need to calculate when ||r(t)|| is min and max on the interval. It might be easier to work with ||r(t)||² and remember that the max and min of a function on a closed interval might occur at a critical point or an end point.

I am still stumped on part (d), I am using Derive 6 to derive,simplify the problems.

Where are you stuck?

$$F(t) =||r(t)||^2 =\sin^2 \pi t+ \ln^2(t) +\frac 1 {16} e^{2t},\ <br /> \frac 1 4 \leq t \leq e$$

Don't you know how to use max/min problems in calculus? The possible values of t are critical points and end points.

 

[danpiz23]

No, not sure if that was something we went over in calc 1, but calc 2 was all derivatives and integration. Calc 3 just started and so far it's been vector calc and distance between point/plane, plane/plane and point/line.
I was able to get
$$F(t) =||r(t)||^2 =\sin^2 \pi t+ \ln^2(t) +\frac 1 {16} e^{2t},\ <br /> \frac 1 4 \leq t \leq e$$

Do I just plug in (1/4) and then e for t? What do I do with those values?

 

[LCKurtz]

No, not sure if that was something we went over in calc 1, but calc 2 was all derivatives and integration. Calc 3 just started and so far it's been vector calc and distance between point/plane, plane/plane and point/line.
I was able to get
$$F(t) =||r(t)||^2 =\sin^2 \pi t+ \ln^2(t) +\frac 1 {16} e^{2t},\ <br /> \frac 1 4 \leq t \leq e$$

Do I just plug in (1/4) and then e for t? What do I do with those values?

Why don't you start by drawing a graph of that? I presume your software will do that. It will show you where your max and min points are. Then look in your Calc I or II book and review where it talks about critical points and finding the relative extrema of functions.

 

[danpiz23]

Why did you use ||r(t)||^2 instead of ||r(t)||?

Can I use the graph of ||r(t)|| to find the max and min?

 

[LCKurtz]

Why did you use ||r(t)||^2 instead of ||r(t)||?

Can I use the graph of ||r(t)|| to find the max and min?

Because it is easier to work with without the square root. Both the function and its square will have maximum or minimum for the same value of t. You will see when you find the critical point. If you are doing it all with software, it probably makes no difference.