- #1
Jtechguy21
- 51
- 0
Homework Statement
Hello, I just started my summer class "Applied Linear Algebra I"
Last math class of my under-grad and its been 1 year since I've last taken Calc3, so I'm trying my best to get back into the groove...anyways.
Our first topic we are discussing in class is vectors.
[1]
This is all the information give to me.
Consider the Vector v = [x y] or <x, y > (which ever notation you prefer)
Find the components of the vector obtained by rotating v about the origin counter clockwise through an angle of 30 degrees.
Homework Equations
The Attempt at a Solution
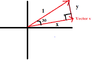
Vector v lives in Quadrant 1, and therefore all I know is that x, and y are positive.So I rotate vector v by 30 degrees counter clock wise.
(Attached rough sketch)
I'm not sure what to do next but this is what I believe.
cos 30 = (square root of (3) )/ 2
sin 30 = 1/2
cos 30 = x / 1 (CAH)
sin 30 = y /1 (SOH)
Answer 1]
Components of vector v = <x,y>
Answer 2]
Components of vector v = < cos30, sin30 >
Can someone please tell me if I am on the right track.
thanks any guidance towards the right direction is greatly appreciated. I am here to learn.